Projeção e Reflexão Ortogonal e Mínimos Quadrados
À questão “Em , determine a projeção ortogonal de sobre o plano gerado pelos vetores e ”, Andrezinho respondeu da seguinte maneira:
Defina o que é a projeção ortogonal sobre um subespaço .
Determine a projeção ortogonal de sobre o plano .
Andrezinho respondeu que a projeção ortogonal de é um vetor de ! Explique o erro de Andrezinho e a que vetor corresponde.
Calcule a distância de à sua projeção sobre o plano .
Passo 1
Letra
Basta trocar o espaço vetorial por e por .
Passo 2
Letra
Poderíamos calcular a transformação linear , entretanto daria muito mais trabalho visto que no enunciado já começaram a calcular por mínimos quadrados. Assim sendo, vamos continuar o raciocínio de Andrezinho.
Sabemos que nos mínimos quadrados:
A projeção é calcula da seguinte forma:
Assim, o vetor seria a solução dos mínimos quadrados e não a projeção do vetor em si.
Assim, basta fazer:
Assim, o vetor projeção é .
Passo 3
Letra
Andrezinho errou, ao falar que a projeção de um vetor do dá um vetor no , logo Andrezinho não sabe usar o método dos mínimos quadrados.
Podemos dizer que o vetor significa a solução dos mínimos quadrados que melhor aproximaria a solução do sistema original, ou também que carrega as coordenadas do vetor na base .
Passo 4
Letra
Sabemos que a distância entre dois vetores ,por exemplo, é calculada da seguinte forma:
Assim para saber a distância pedida no enunciado basta fazer:
Se você estiver com dificuldade de visualizar, basta fazer o desenho e depois a regra do paralelogramo! É mais ou menos isso aqui:
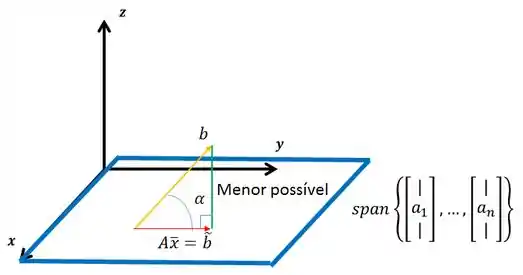
Assim o vetor distância é:
Portanto, a distância em si é dada por:
Resposta
;
Projeção e uso dos mínimos quadrados;
.