A3 T15
Sejam um espaço vetorial com produto interno e o conjunto linearmente independente e seja a projeção de em . Então:
é ortogonal a
é ortogonal a
Passo 1
Esse desenho lindo e maravilhoso que você pode fazer rapidamente na sua prova tem todas as respostas que precisamos:
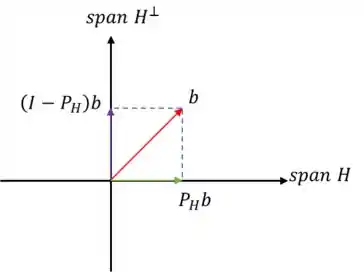
Ta, vamos adaptar ele para o nosso problema! Temos o seguinte:
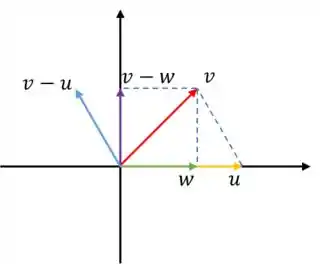
Só com isso já dá pra responder o problema né?
. Essa é falsa. (na verdade seria igual se , mas como não podemos sempre afirmar isso, essa é falsa).
. Tenho nem o que falar, muito falsa essa haha.
não é ortogonal a . Falsa também.
é ortogonal a . Agora sim, essa faz sentido! Se é a projeção de em , será a projeção de em . Então ele sempre vai ser perpendicular a !
Resposta
Letra
Exercícios de Livros Relacionados
1. Calcular o centróide dos vetores e representar geometricamente: u 1 = 1,2 e u 2 = 2,1 ; u 1 = 1,1 , u 2 = 1,2 , u 3 = 4 , - 1 e u 4 = 2,2 ; u 1 = 1,2 , 1 , u 2 = - 1 , - 2,0 e u 3 = 0,0 , - 1 ; u 1
3. Enunciar rigorosamente e provar: um operador linear do R n preserva os centróides.
4. Tomemos três vetores no R 2 , cujas extremidades formem um triângulo. Qual é o ponto do triângulo que coincide com a extremidade do centróide dos três vetores?
2. Seja u o centróide dos vetores u 1 , u 2 , … , u p do R n . Calcular nos exemplos do exercício 1 a soma u - u 1 2 + … + u - u p 2 .
Qual é a série de Fourier de s e n (3 x) ?