Água escoa suavemente pela tubulação cilíndrica da figura ao lado, preenchendo-a completamente.
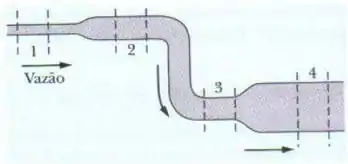
As secções 2 e 3 têm o mesmo diâmetro. Como podemos relacionar as velocidades em cada região?
Passo 1
Pelo princípio da continuidade, toda água que entra por unidade de tempo tem que sair na mesma vazão. Daí tiramos que
Onde v é a velocidade naquele ponto e A é a área da seção reta da tubulação.
Ou seja, a velocidade é maior quanto menor for a área. Por isso que a velocidade da água aumenta quando você bota o dedo na saída de uma mangueira de água.
Passo 2
Como 2 e 3 possuem o mesmo diâmetro, então . Pelo princípio da continuidade:
Então .
Como em 1 a área é menor que em 2.
Então
E em 4 a área é maior que em 2,
Juntando tudo:
Resposta
B)
Exercícios de Livros Relacionados
A água que sai de um cano de 1,9c m (diâmetro interno) passa por três canos de 1,3c m . (a) Se as vazões nos três canos menores são 26 , 19 e 11L / m i n , qual é a vazão no tubo de 1,9c m ? (b) Qual
Dois riachos se unem para formar um rio. Um dos riachos tem um largura de 8,2m , uma profundidade de3,4m e a velocidade da água é 2,3m / s . Outro riacho tem 6,8m de largura , 3,2m de profundidade e a
a) Sabendo que um certo volume de água flui por uma mangueira com diâmetro d 1 = 3,0 cm e com velocidade de fluxo igual a v 1 = 0,65 m/s até a extremidade de um bocal com diâmetro d 2 = 0,30 cm, qual
A água escoa em um tubo cilíndrico cuja seção reta possui área variável. A água enche completamente o tubo em todos o spontos. a) Em um ponto o raio do tubo é igual a 0,150m. Qual é a velocidaded da á
A água escoa em um tubo cuja seção reta possui área variável e enche completamente o tubo em todos os pontos. No ponto 1, a seção reta possui área igual a 0,070 m 2 e o modulo da velocidade do fluido