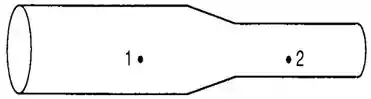
Em um escoamento, o tubo circular por onde passa um fluido é estrangulado e seu diâmetro reduz-se à metade. O que acontece com a velocidade do fluido?
Passo 1
Queremos saber como a velocidade do fluido varia quando o diâmetro do tubo é reduzido á metade.
Pela equação da continuidade:
Passo 2
Como se trata de um tubo, podemos calcular as áreas em função dos diâmetros:
Passo 3
Substituindo na equação da continuidade:
Separando velocidades para um lado e os diâmetros para o outro:
Passo 4
Agora podemos substituir a relação entre os diâmetros.
Como o diâmetro reduz-se à metade, então:
Ou seja:
Passo 5
Substituindo na expressão que encontramos:
Logo, a velocidade após o estrangulamento é multiplicada por .
Resposta
A velocidade quadruplica.
Exercícios de Livros Relacionados
A água que sai de um cano de 1,9c m (diâmetro interno) passa por três canos de 1,3c m . (a) Se as vazões nos três canos menores são 26 , 19 e 11L / m i n , qual é a vazão no tubo de 1,9c m ? (b) Qual
Dois riachos se unem para formar um rio. Um dos riachos tem um largura de 8,2m , uma profundidade de3,4m e a velocidade da água é 2,3m / s . Outro riacho tem 6,8m de largura , 3,2m de profundidade e a
a) Sabendo que um certo volume de água flui por uma mangueira com diâmetro d 1 = 3,0 cm e com velocidade de fluxo igual a v 1 = 0,65 m/s até a extremidade de um bocal com diâmetro d 2 = 0,30 cm, qual
A água escoa em um tubo cilíndrico cuja seção reta possui área variável. A água enche completamente o tubo em todos o spontos. a) Em um ponto o raio do tubo é igual a 0,150m. Qual é a velocidaded da á
A água escoa em um tubo cuja seção reta possui área variável e enche completamente o tubo em todos os pontos. No ponto 1, a seção reta possui área igual a 0,070 m 2 e o modulo da velocidade do fluido