Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Princípio da Continuidade

Ver Teoria
Exercício 25123456789101112131415161718192021222324

Enunciado

PUCRIO – Física 2 2020.1 – G1– Questão 8

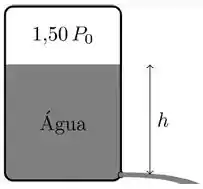
O interior de uma caixa d’água contém um gás a uma pressão P = 1,50   P 0 ( P 0 é a pressão

atmosférica). A uma profundidade h = 1,51   m   com relação ao nível da água é feito um furo de área muito pequena quando comparado a área da caixa d’água. Supondo que a área do furo seja tal que sua vazão fique em R V   =   1,00 ×   10 - 4   m 3 / s .

a) Encontre a velocidade de saída da água através desse furo.

h , mas com o dobro da área do primeiro furo (mas ainda muito menor que a área da caixa d’água), qual será o novo valor da vazão?

Passo 1

Fala galera, tudo bem? Vou ajudar você a resolver essa questão! Vamos lá?

Letra (a):

Vamos usar a equação da continuidade:

P 1 + ρ g y 1 + 1 2 ρ v 1 2 = P 2 + ρ g y 2 + 1 2 ρ v 2 2

Temos que a área do tanque é muito maior que a área do furo, então podemos supor que a velocidade no topo do tanque v 1 é zero. Vamos também considerar que a caixa d´água está no chão, então y 2 = 0 . A pressão na saída do furo é a pressão atmosférica P 0 , então podemos substituir esses dados e simplificar alguns termos:

1,5 P 0 + ρ g h = P 0 + 1 2 ρ v 2 2

E daqui podemos calcular a velocidade v 2 :

1,5 P 0 - P 0 + ρ g h = 1 2 ρ v 2 2

v 2 2 = 2 ρ 1,5 P 0 - P 0 + ρ g h  

v 2 = 2 ρ 0 , 5 P 0 + ρ g h  

Os valores são:

ρ = 1000

P 0 1,01 × 10 5

g = 9,8

h = 1,51

a velocidade é:

v = 2 1000 0,5.1,01 × 10 5 + 1000 9,8 ( 1,51 )

v = 121,81 m / s

Tranquilo até aqui?

Passo 2

Letra (b):

A velocidade não vai ser alterada, então a primeira vazão é:

R v = v A 1

v = R v A 1

E a segunda vazão é:

R = v A 2

R = R v A 1 A 2

Mas A 2 = 2 A 1 :

R = R v 2 A 1 A 1 = 2 R v

Então a nova vazão será duplicada:

R = 2 × 10 - 4 m 3 / s

Beleza?

Pronto pra próxima questão? =)

Resposta

a ) v = 121,81 m / s

b ) R = 2 × 10 - 4 m 3 / s

Exercícios de Livros Relacionados

A água que sai de um cano de 1,9c m (diâmetro interno) passa por três canos de 1,3c m . (a) Se as vazões nos três canos menores são 26 , 19 e 11L / m i n , qual é a vazão no tubo de 1,9c m ? (b) Qual
Dois riachos se unem para formar um rio. Um dos riachos tem um largura de 8,2m , uma profundidade de3,4m e a velocidade da água é 2,3m / s . Outro riacho tem 6,8m de largura , 3,2m de profundidade e a
a) Sabendo que um certo volume de água flui por uma mangueira com diâmetro d 1 = 3,0 cm e com velocidade de fluxo igual a v 1 = 0,65 m/s até a extremidade de um bocal com diâmetro d 2 = 0,30 cm, qual
A água escoa em um tubo cilíndrico cuja seção reta possui área variável. A água enche completamente o tubo em todos o spontos. a) Em um ponto o raio do tubo é igual a 0,150m. Qual é a velocidaded da á
A água escoa em um tubo cuja seção reta possui área variável e enche completamente o tubo em todos os pontos. No ponto 1, a seção reta possui área igual a 0,070 m 2 e o modulo da velocidade do fluido