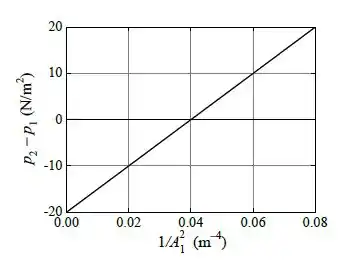
Um fluido ideal com densidade escoa horizontalmente do segmento 1 de uma tubulação, com seção reta , para o segmento 2, com seção reta . A variação de pressão com a altura é desprezível. A figura abaixo mostra o gráfico da diferença e pressão em função de , para um valor fixo de .
- Determine o valor de em metros quadrados.
- Quantos metros cúbicos do fluido são escoados através de uma seção reta da tubulação no intervalo de um minuto?
(Dados: ;)
Passo 1
Da equação de Bernoulli temos:
Agora, da Equação da Continuidade:
Substituindo para e :
Show!
Passo 2
Agora que vem o pulo do gato! Do gráfico, vemos que a diferença de é nula quando:
Mas por que isso acontece? A diferença de pressão é devida à diferença de velocidades, que é devida à diferença de áreas (porque estamos na mesma altura sempre). Então quando a diferença de pressão for zero, não haverá diferença de áreas, sacou?
Logo temos que o valor de é:
Passo 3
b) Vamos analisar o gráfico para obter a informação da quantidade de fluído que escoa no intervalo de 1 minuto.
Quando, , temos que
Logo:
Portanto a variação de volume em 1 minuto é:
Resposta
a)
b)