Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Quádricas

Ver Teoria
Exercício 1012345678911121314151617181920

Enunciado

UFPE – Geometria Analítica – 2018.1 – P3 – Questão 2

Considere a quádrica

Ω :   - x 2 - 4 y 2 + 4 z 2 + 2 x + 16 y = 21

  1. Identifique e esboce a quádrica Ω .
  2. Identifique a cônica Τ = Ω ⋂ π , indicando as coordenadas de seus focos, nos casos em que π :   x - 1 = 0 e π :   z + 2 = 0 .

Passo 1

  1. Vamos desenvolver essa expressão da quádrica, pra tentarmos deixar naquele formato dos quadrados, que estamos mais acostumados.

    2. - x 2 - 4 y 2 + 4 z 2 + 2 x + 16 y = 21

    - x 2 - 2 x - 4 y 2 - 4 y + 4 z 2 = 21

    - x 2 - 2 x + 1 - 4 y 2 - 4 y + 4 + 4 z 2 = 21 - 1 - 16

    - x - 1 2 - 4 y - 2 2 + 4 z 2 = 4

    - x - 1 2 4 - y - 2 2 + z 2 = 1

    Três termos ao quadrado dando uma parada constante positiva, sendo que dois sinais são negativos: isso é a equação de um hiperboloide de duas folhas, com centro em ( 1 ,   2 ,   0 ) . O termo com sinal positivo é o z , então nele que vai ficar o eixo de simetria!

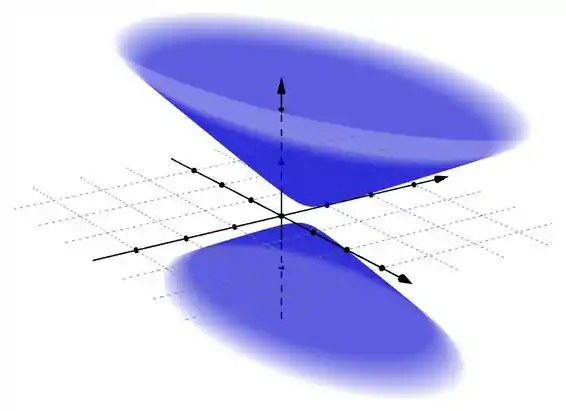
    Passo 2

  2. Agora vamos intersectar a quádrica com esses dois planos. Primeiro, para o plano π : x = 1 ,

- y - 2 2 + z 2 = 1 x = 1

Essa equação determina uma hipérbole no plano x = 1 . Essa hipérbole tem a e b iguais a 1 , e portanto, pela relação fundamental:

c 2 = 1 2 + 1 2

c = 2

O centro da hipérbole está em ( 1 ,   2 ,   0 ) , e assim, como o eixo de simetria é o eixo z , os focos tem coordenadas:

F 1 = 1 ,   2 ,   - 2

F 2 = 1 ,   2 ,   2

Passo 2

Ainda na letra (b), vamos resolver o segundo caso, para o qual π :     z = - 2 ,

- x - 1 2 4 - y - 2 2 + - 2 2 = 1

- x - 1 2 4 - y - 2 2 = - 3

x - 1 2 12 + y - 2 2 3 = 1 z = - 2

Essa equação determina uma elipse no plano z = - 2 . Essa elipse tem a 2 = 12 e b 2 = 3 , e portanto, pela relação fundamental:

12 = 3 + c 2

c = 3

O centro da elipse está em ( 1 ,   2 ,   3 ) , e como o eixo maior é o eixo x , os focos são:

F 1 = ( - 2,2 , - 2 )

F 2 = 4,2 , - 2

Resposta

  1. - x - 1 2 4 - y - 2 2 + z 2 = 1 : hiperboloide de duas folhas
  2. No plano π : x = 1 , a cônica é uma hipérbole de focos   F 1 = 1 ,   2 ,   - 2 e   F 2 = 1 ,   2 ,   2 . No plano π : z = - 2 , a cônica é uma elipse de focos F 1 = ( - 2,2 , - 2 ) e F 2 = 4,2 , - 2 .

Exercícios de Livros Relacionados

Escolhendo convenientemente os eixos, mostre que a interseção de um plano com uma quádrica central é uma cônica. Em particular, mostre que a interseção de um plano com um elipsoide é uma elipse.
Escreva as equações de mudança de eixos (rotações) que eliminam os termos em x y ,x zey z nas formas quadráticas do Exercício 44.1.
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y