Considere a quádrica de equação
Determine uma base que gera um sistema de coordenadas no qual essa quádrica tem uma equação livre de termos quadráticos mistos e então identifique-a.
Passo 1
Belezera galerinha, o enunciado deu pra gente a quádrica:

E pede pra gente encontrar uma base que gera um sistema de coordenadas no qual essa quádrica tem uma equação livre de termo quadráticos mistos, e então é pra gente identificar o que é essa tal quádrica...

Mas calma lá galerinha, vamos com amor e com carinho. A nossa intenção aqui é reescrever essa quádrica livre dos termos quadráticos mistos, que na verdade são esses aqui ó:
![]()
A gente chama eles de “mistos” pelo fato de serem uma multiplicação entre duas variáveis distintas, e a gente não quer isso!! O problema é que essa quádrica está escrita na base canônica, e por esse fato esses termos mistos ficam aparecendo, MAAASSS se por acaso a gente encontrasse uma base diferente da canônica que pudéssemos reescrever a quádrica tal que desaparecesse esses termos mistos, Albert Einstein iria se remexer de inveja no túmulo.

Então é justamente isso que iremos fazer. Come here!
Passo 2
Vamos separar primeiro essa quádrica em duas partes, assim ó:
Podemos reescrever o primeiro termo entre parênteses em termos matriciais, mas primeiro vamos entender como se faz isso. O primeiro polinômio tem uma expressão geral dada como:
E quando isso acontece podemos decompor a quádrica como:
Onde:
Trazendo para o nosso caso:
Dessa forma, descobrimos que a decomposição fica:
Show de bolas, então já conseguimos reescrever o primeiro termo entre parênteses. Agora o segundo termo é um pouquinho mais simples, podemos chamar ele de:
Logo, se a gente juntar tudo, descobrimos que a nossa quádrica escrita em forma matricial é:
E então a única quádrica de verdade existente agora é essa daqui:
Vamos analisar ela.

Passo 3
Agora, precisamos encontrar uma base que é diferente da canônica e que mantém as características no espaço, ou seja, que preserve as direções da quádrica no espaço. E é aí que tá a malícia, porque os vetores que preservam as direções no espaço mesmo após a aplicação da transformação são os nosso conhecidos autovetores!! Então encontrar a base que nos ajude no nosso milagre, é encontrar uma base ortonormal de autovetores que diagonaliza a matriz da forma quádrica. Então podemos pegar a matriz:
E encontrar os autovetores dessa matriz, através da relação:
Onde os valores de serão os nossos autovalores. E pra facilitar nossos cálculos, podemos fazer duas operaçõezinhas na nossa matriz afim de tornar ela mais bonitinha. Primeiro, podemos zerar o termo que aparece na coordenada . Pra isso, vamos dividir a primeira linha por , multiplicar ela por para então somar com a linha 2, desse jeito:
Agora bora zerar o outro termo na coordenada , pra isso podemos fazer parecido com o anterior, só que agora precisamos multiplicar a linha 2 por e depois por novamente, para poder somar com a linha 3, desse jeito:
Portanto, agora podemos calcular o determinante somente multiplicando os elementos da diagonal principal:
E como num passe de mágica, SIMSALAMBIM!
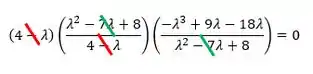
Colocando o em evidência, temos:
Iradoso, já temos uma raiz em , e resolvendo a equação do segundo grau dentro dos parênteses, obtemos:
Portanto, os autovalores da matriz da forma quádrica é são , e .
Passo 4
Sabendo disso, podemos então encontrar os autovetores associados a esses autovalores, saca só, para , temos:
E o conjunto solução desse sistema é:
O autovetor é , e se normalizarmos ele, chegamos em:
Para temos que:
E a solução do sistema é:
E nosso autovetor é que possui a mesma norma do outro, portanto ele normalizado é:
E por fim para o autovalor , temos:
Cujo autovetor respectivo é . Normalizando ele, obtemos:

Então nossa base ortonormal é:
Passo 5
Agora que vem a parte legal, porque isso quer dizer que podemos reescrever nossas variáveis como uma combinação dos vetores da base , ou seja, estamos mudando de base da canônica para a . Ficando assim:

Então quer dizer que podemos reescrever toda aquela nossa quádrica do início:
Nas variáveis , e desse jeito:
E finalmente, depois de pagar todos os pecados que o mundo já cometeu, resolvendo esse produto em matrizes chegamos que:

Então conseguimos reescrever a quádrica sem os termos mistos, e ainda de quebra descobrimos que ela é um parabolóide elíptico.