Encontre as coordenadas dos focos da elipse que resulta da interseção de com
.
Passo 1
O enunciado já fala que a interseção do parabolóide elíptico com o plano será uma elipse. Então, para achar a elipse resultante basta substituirmos na equação do paraboloide. Ficaremos com:
Deixando na forma canônica, teremos:
Passo 2
Já temos a expressão da elipse, agora, precisamos encontrar as coordenadas dos focos. Lá da teoria de “Cônicas” temos o seguinte resumo:
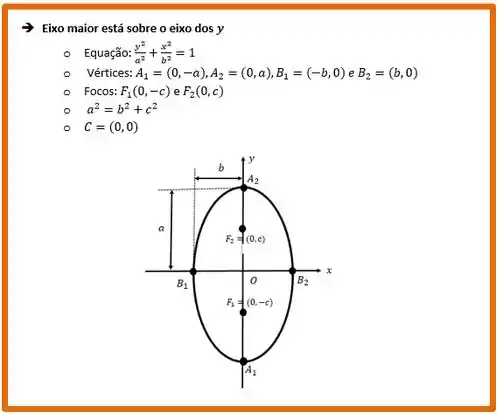
Como o maior valor do denominador está sobre o , então realmente estamos no caso em que o eixo maior está sobre o eixo do .
Vamos então, primeiro retirar os valores que precisamos. Da expressão:
Temos que:
Usando a relação do resumo acima encontramos o valor de :
E todas essas contas que fizemos valem para ! Então, as coordenadas dos focos da elipse serão:
Acabouuuu!!!
Esse tipo de exercício é importante para percebermos como os assuntos estão conectados e que devemos estar com a teoria afiada ;).