Considere a quádrica
a) Identifique e esboce .
b) Determine todos os 6 planos paralelos a algum plano coordenado que intersectam em uma cônica com distância focal .
Passo 1
a) Podemos escrever nossa equação assim:
Isso é a mesma coisa que
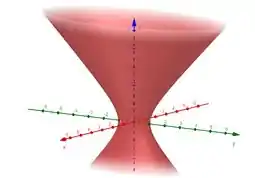
Boaa, agora sim estamos na nossa forma usual :D Isso aí é a equação de um hiperboloide de uma folha não é? Afinal temos 2 sinais positivos e 1 negativo :P
Lembrando que como o é o negativo, o hiperboloide está ao longo do eixo .
O esboço dele fica assim
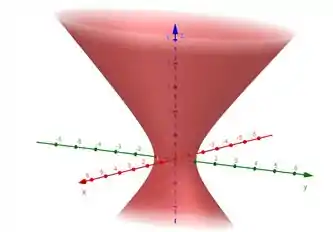
Passo 2
A distância focal tanto da elipse como da hipérbole é certo?
Queremos que , então
Passo 3
Vamos começar fazendo na equação do hiperboloide:
Dividindo tudo por :
Isso dá pra gente a equação de uma elipse, onde os parâmetros são
(lembrando que )
Então
Mas queremos que :
Então, a intersecção dos planos e com nosso hiperboloide, forma elipses com distância focal
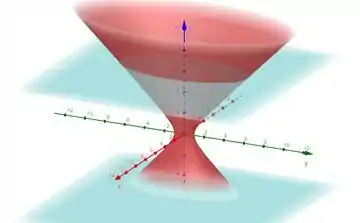
Passo 4
Agora vamos fazer na equação do hiperboloide:
Dividindo tudo por :
Ou:
Temos as equações de duas hipérboles, vamos encontrar seus parâmetros:
Em :
e
Então
Do passo 1:
-> Impossível
Então vamos descartar a equação :P
Em :
e
Então
Do passo 1 temos que
Portanto, em e a intersecção nos dá hipérboles com distância focal
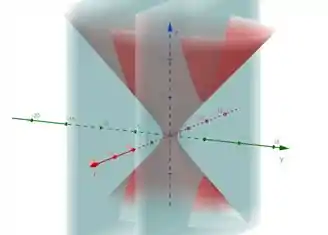
Passo 5
Ufa ta acabando!! Agora só falta fazer na equação do hiperboloide:
Dividindo tudo por :
Ou:
Temos duas equações de hipérboles novamente ok?
Em :
Então
-> Impossível
Então vamos descartar fechou?
Em :
Então a intersecção dos planos e com o hiperboloide, nos dá duas hipérboles com distância focal
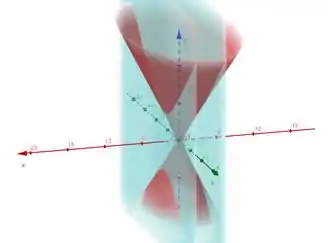
Resposta
a) Hiperboloide de uma folha.
b) e
e
e