Considere a quádrica de equação
onde , são números reais.
a) Para e , identifique a quádrica e esboce o gráfico.
b) Para , identifique a curva obtida pela intersecção da quádrica com o plano e determine seu(s) foco(s).
Passo 1
a) Se e , vamos ter a seguinte equação
Arrumando essa equação e dividindo tudo por 16 vamos ter:
Lá na teoria a gente viu que isso aí é a equação de um cilindro elíptico lembra? Sendo que nesse caso, e .
Então, o gráfico vai ser assim:
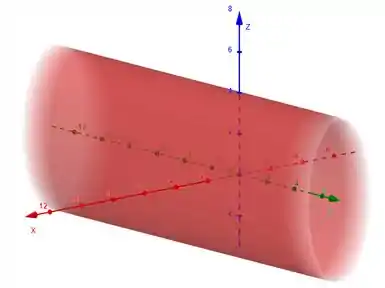
Passo 2
b) Quando , nossa equação vai ser
Pra gente achar a intersecção dessa quádrica com o plano , vamos resolver o sisteminha:
Substituindo na equação de cima:
Então, a intersecção vai ser dada por
Deixando a equação mais ajeitadinha teremos:
Essa é a equação de uma hipérbole, que como não possui variável mas pertence à intersecção com o plano , ela está CONTIDA nesse plano.
Nessa equação, temos , e .
Os focos dessa hipérbole vão ser e , então:
Resposta
a)
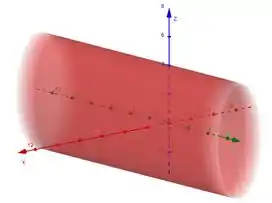
b) Hipérbole com focos: