Exercícios Resolvidos de Quádricas

Exercício 5 1 2 3 4 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

Enunciado

Considere a quádrica e a curva que é a intersecção de com o plano .

a) Identifique .

b) Identifique .

c) Determine os elementos geométricos de tais como vértices, focos, assíntotas e diretriz.

d) Faça um esboço de .

Passo 1

a) Para encontrarmos , vamos completar quadrados:

Isso nos dá

Dividindo tudo por 36, temos

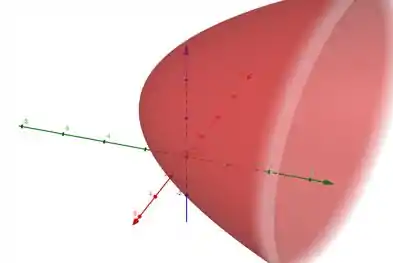
Essa equação reduzida nos mostra que é um paraboloide elíptico, com vértice no ponto e eixo paralelo ao eixo . Seu esboço ta na figura abaixo

Passo 2

b) A curva é a intersecção de com o plano . Então a gente tem que fazer na equação de :

Isso dá pra gente a equação de uma parábola :)

Passo 3

c) O vértice da nossa parábola vão ser as coordenadas que subtraem de e , ou seja, .

O parâmetro está no denominador de em formato de , ou seja, .

O foco vai ser .

Então a diretriz de vai ser a reta .

Passo 4

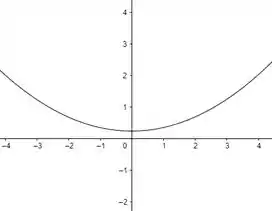
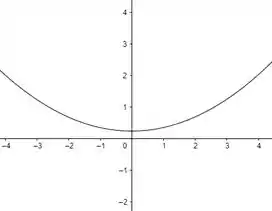
d) Abaixo temos um esboço da parábola :

Resposta

a) Parabolóide elíptico.

b) Parábola.

c)

Diretriz:

d)

Exercícios de Livros Relacionados

Escolhendo convenientemente os eixos, mostre que a interseção de um plano com uma quádrica central é uma cônica. Em particular, mostre que a interseção de um plano com um elipsoide é uma elipse.

Escreva as equações de mudança de eixos (rotações) que eliminam os termos em x y ,x zey z nas formas quadráticas do Exercício 44.1.

Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y

Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y

Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y