Identifique a quádrica e esboce a intersecção de com o plano , determinando o centro e os focos da cônica .
Passo 1
Vendo a equação dessa quádrica, a gente já repara que ela ta trasladada certo? Então vamos completar quadrados em :
Podemos escrever isso assim:
Isso é a mesma coisa que
Dividindo tudo por e simplificando:
Ebaaa, achamos a nossa quádrica , e ela é um hiperboloide de duas folhas, pois temos dois sinais negativos :P
Passo 2
Agora vamos encontrar a intersecção de com o plano .
Sabemos que o plano também pode ser escrito como , então vamos pegar a equação de e substituir por :
Dividindo tudo por :
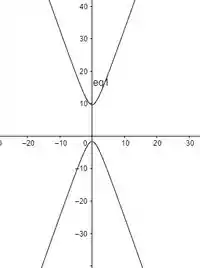
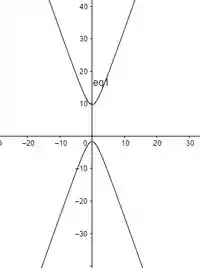
A cônica é uma hipérbole com centro em (lembrando que ela está no plano ) e ao longo do eixo , que está positivo na equação.
Os parâmetros geométricos dessa hipérbole são
Os focos dessa hipérbole serão
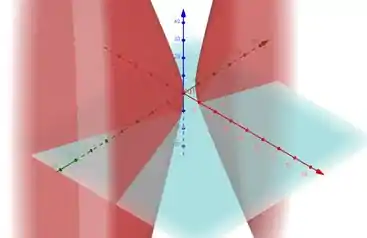
Abaixo temos o desenho da quádrica e o plano .
Abaixo temos o esboço da hipérbole formada pela intersecção dos dois
Resposta
(hiperboloide de duas folhas)
(hipérbole)