UFPE – Geometria Analítica – 2018.2 – P3 – Questão 3
Considere a quádrica de equação
- Identifique e esboce
- Determine a interseção de com o plano . Caso essa interseção seja uma cônica não degenerada (elipse, parábola ou hipérbole), determine seus vértices e focos.
Passo 1
- Pra identificar a quádrica, vamos primeiro completar quadrados, como sempre!
- Como a gente pode ver na figura, a seção em é uma elipse! Substituindo na equação:
Isso é a equação de um elipsoide de revolução! Seu centro encontra-se no ponto .
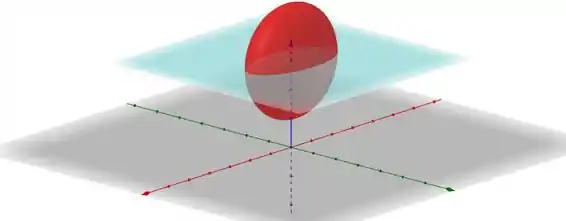
Passo 2
Essa elipse tem parâmetros geométricos:
Da relação fundamental:
O eixo maior é o eixo e o eixo menor o eixo ! Então seus vértices e focos vão ser os seguintes (não esquece que estão todos em ):
Resposta
Exercícios de Livros Relacionados
Escolhendo convenientemente os eixos, mostre que a interseção de um plano com uma quádrica central é uma cônica. Em particular, mostre que a interseção de um plano com um elipsoide é uma elipse.
Escreva as equações de mudança de eixos (rotações) que eliminam os termos em x y ,x zey z nas formas quadráticas do Exercício 44.1.
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y