Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Quádricas

Ver Teoria
Exercício 7123456891011121314151617181920

Enunciado

Considere a quádrica

Q :   16 x 2 - 9 y 2 - 16 z 2 + 32 x + 36 y - 64 z - 228 = 0

a) Identifique Q .

b) Determine o centro de Q .

c) Esboce Q .

d) Justifique se Q é ou não uma superfície de revolução.

Passo 1

a) Vamos completar os quadrados na equação de Q :

16 x 2 + 2 x + 1 - 9 y 2 - 4 y + 4 - 16 z 2 + 4 z + 4 - 228 = 16 - 36 - 64

16 x + 1 ² - 9 y - 2 ² - 16 z + 2 ² = 144

Dividindo tudo por 144:

16 x + 1 ² 144 - 9 y - 2 ² 144 - 16 z + 2 ² 144 = 1

x + 1 ² 9 - y - 2 ² 1 6 - z + 2 ² 9 = 1

Isso nos dá a equação de um hiperboloide de duas folhas :)

Passo 2

b) Observando os números que subtraem x , y e z na equação de Q , temos que o seu centro é C = ( - 1 ,   2 ,   - 2 ) .

Passo 3

c) Nosso hiperboloide vai estar ao longo do eixo x , que está positivo na equação:

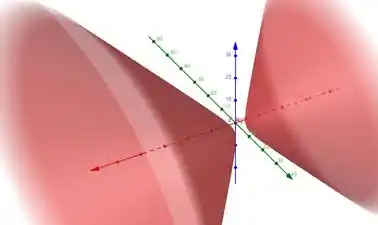
Passo 4

Passo 5

d) Não é uma superfície de revolução, pois os cortes/traços que se interseccionam com a figura e não formam hipérboles, formam elipses no plano x = k com k > 2 ou k < - 4 .

Resposta

a) Hiperboloide de duas folhas.

b) C = ( - 1 ,   2 ,   - 2 )

c)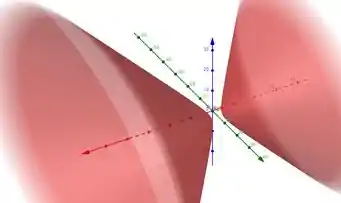

d) Não é uma superfície de revolução, pois os cortes/traços que se interseccionam com a figura e não formam hipérboles, formam elipses no plano x = k com k > 2 ou k < - 4 .

Exercícios de Livros Relacionados

Escolhendo convenientemente os eixos, mostre que a interseção de um plano com uma quádrica central é uma cônica. Em particular, mostre que a interseção de um plano com um elipsoide é uma elipse.
Escreva as equações de mudança de eixos (rotações) que eliminam os termos em x y ,x zey z nas formas quadráticas do Exercício 44.1.
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y
Para cada uma das equações abaixo, efetue uma rotação de eixos de modo a eliminar os termos em x y ,x z ,y z . Em seguida, efetue translações de modo a eliminar, ou reduzir a um só, os termos em x, y