a) Em um experimento de fenda dupla, a abertura de cada fenda vale e distância entre as fendas é . Incide-se luz de comprimento e onda de perpendicularmente ao plano das fendas. Faça um gráfico da intensidade da luz em função de , sendo o ângulo de chegada dos raios no anteparo, em relação ao eixo central, incluindo ao menos as envoltórias até os segundos mínimos de difração. Dentro da envoltória central de difração, ache o valor das intensidades máximas dos picos de interferência, relativos àquela para .
b) Uma rede de difração tem o espaçamento entre fendas igual a . Ache a dispersão da rede em máximos de 1ª ordem e assim encontre a abertura angular entre comprimentos de onda incidentes de e . Para, nessas condições, ser capaz de resolver esses comprimentos de onda, qual deve ser o número mínimo de fendas da rede?
Passo 1
Eai galerinha, prontos para resolver uma questão de física 4?
No item (a) desse problema vamos discutir o problema da difração por uma dupla fenda. Para isso, temos que lembrar que a intensidade é dada por
O termo com o ângulo é responsável pela envoltória enquanto o termo com é responsável pelos máximos e mínimos de interferência.
O primeiro passo é achar os mínimos da envoltória. Para isso, queremos achar os valores de tais que
Observe que não é um desses valores pois tomando o limite a expressão acima dá , não . Para devemos ter
Substituindo a expressão de :
A seguir eu faço um plot dessa envoltória com os mínimos em função de :
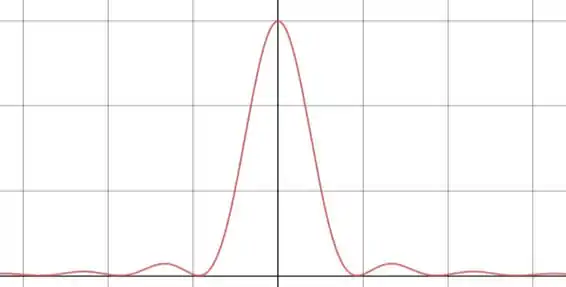
Observe que a envoltória central tem amplitude bem maior que as demais. É por isso que apenas a região central é visível nesse tipo de experimento. Os pontos em que a curva se anula são
Passo 2
Dentro dessa envoltória o segundo termo vai oscilar. Para achar os máximos dessa oscilação, temos que resolver a equação:
Logo, usando a expressão para apresentada no passo 1:
Portanto, os máximos de interferência ocorrem para
Vamos ver quantos máximos desse tipo ocorrem na envoltória central. Para isso, queremos que
Simplificando e multiplicando por :
Como e , temos que
Com isso, os máximos acontecem para . Desta forma, vemos que dentro da envoltória central temos 5 máximos de interferência. A seguir faço o esboço da curva de intensidade:
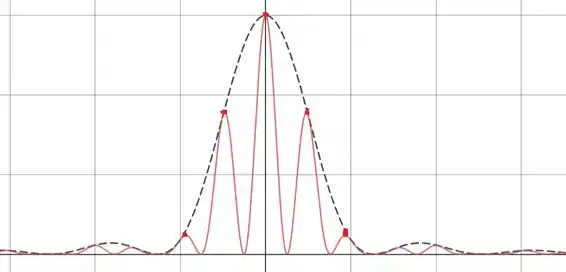
Os máximos de interferência na envoltória central estão marcados em vermelho.
Passo 3
Para terminar o item (a), temos que achar as intensidades os máximos de interferência dentro da envoltória central. Para todos esses máximos, temos que
Com isso,
Mas sabemos também que esses máximos acontecem para
Substituindo na expressão para a intensidade:
Usando os valores de e :
Portanto,
Sabemos que para o limite dá
Isso significa que é a intensidade máxima. Vamos achar as intensidades relativas dos demais máximos com e . No primeiro caso:
Já no segundo:
Vemos que a intensidade dos máximos de segunda ordem é bem menor que as intensidades dos máximos central e de primeira ordem.
Passo 4
Agora que finalizamos o item (a) podemos partir para o item (b)!
Nesse item vamos brincar com uma rede de difração. Primeiro queremos achar a dispersão para máximos de primeira ordem. A dispersão é definida por
Para ângulos pequenos, temos , de modo que
Usando (1ª ordem) e :
Para achar a abertura angular entre os comprimentos de onda e vamos usar
Como , temos que
Passo 5
Para fechar o problema, temos que encontrar o número mínimo de fendas para conseguir distinguir as franjas de dois comprimentos de onda diferentes com . Para isso, usamos o critério de Rayleigh que encontra a seguinte expressão:
Essa expressão foi dada no enunciado. Como e :
Portanto, são necessárias 200 fendas para conseguir resolver esses dois comprimentos de onda! E assim terminamos o problema 😉!