Uma rede de difração tem uma resolução .
- Mostre que a diferença de frequências que se encontra no limite da resolução, , é dada por .
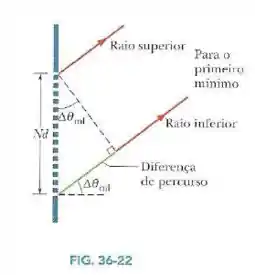
- Para a Fig. 36-22, mostre que a diferença entre os tempos de percurso do raio de baixo e do raio de cima é dada por .
- Mostre que e, portanto, esse produto não depende dos parâmetros da rede. Suponha que .
Passo 1
Letra a)
Para transformar de comprimento de onda em frequência, nós usamos a velocidade da luz:
Assim:
Passo 2
Substituindo o valor nas fórmulas de resolução:
Considerando que , podemos escrever:
Considerando que é muito pequeno, podemos desprezá-lo nas equações e fazer:
De uma forma mais exata, poderíamos usar direto a fórmula do e fazer:
Que recai na anterior se aproximarmos:
Passo 3
Letra b)
Pela figura dada, podemos ver que a diferença de percurso entre os raios do topo e de baixo é:
Quando temos fendas, a distância entre a superior e a de baixo é mas, quando é muito grande, podemos aproximar por .
Seja o percurso de cima e o percurso de baixo. Com a velocidade da luz sendo , os tempos são dados por:
Passo 4
Letra c)
Multiplicando os dois:
Como estamos olhando a resolução das franjas de interferência, nesse caso temos, para ambos e que vale a condição de máximo:
Usando a nossa aproximação de desprezível, podemos dizer que:
Que também nos faz dizer que .
Temos finalmente:
Resposta
Ei, a resposta está no passo a passo :)