A linha D do espectro de Sódio é um dubleto (duas linhas próximas) com comprimentos de onda 𝜆1 = 589 𝑛𝑚 e 𝜆2 = 589,6 𝑛𝑚. Uma rede de difração permite observar esse dubleto no limite da resolução. Mais ainda, a terceira ordem (𝑚 = 3) possui um ângulo de 10° com a normal à tela de observação. Determine:
(a) o espaçamento entre as ranhuras.
(b) o número 𝑁 de ranhuras da rede.
Passo 1
Como sabemos que o comportamento entre todas as fendas é a mesma, vamos analisar apenas duas fendas consecutivas e descobrir o seu comportamento
Vamos entender visualmente o que o enunciado está falando
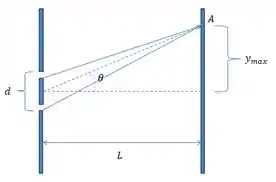
Observamos que no ponto A está ocorrendo uma interferência entre os raios, e no desenho conseguimos compreender cada um dos dados do problema. No nosso exercício onde λ está ligado ao comprimento de onda dos raios, da distancia entre as fendas e L a distancia até o anteparo.
Mas o que o exercício quer?
Ele quer que determinemos a distância angular entre as franjas 1 e 2, ou seja, qual a diferença entre os ângulos dos máximos quando temos m=2.
Passo 2
Sabemos que um máximo de interferência ocorre quando podemos usar a fórmula
Sabemos pelo enunciado que para a ordem de m=3 temos .
Ainda falta definirmos quanto vale o comprimento de onda para substituirmos na equação.
Por critério de aproximação faremos que o comprimento de onda adotado para essa ordem seja a média dos comprimentos de ondas incidentes, logo teremos que
Agora que já temos todos os valores, basta substituirmos na equação e isolarmos o valor de d, pois assim conseguiremos determinar a distância entre as ranhuras.
Passo 3
Sabemos que a fórmula do poder de resolução é dado por
Em que N é exatamente o número de Ranhuras da rede que é o objetivo do nosso item B.
Se isolarmos o valor de N na nossa equação teremos que
Em que os valores são
Substituindo na nossa equação teremos que
Passo 4
Resposta
a)
b)