Um pesquisador quer fabricar uma rede de difração que possa separar dois comprimentos de onda na faixa do azul, e .
a) Qual deve ser a distância entre as fendas sucessivas para que a separação angular entre e seja de para máximos de primeira ordem?
b) Verifique se 200 fendas são suficientes para resolver e em máximos de segunda ordem.
c) Genericamente, para quaisquer comprimentos de onda possam ser distinguidos, explique qualitativamente o critério a ser cumprido.
d) No caso particular da rede de difração, argumente porque a resolução depende do número de fendas e da ordem dos máximos de interferência.
Passo 1
Fala pessoal, prontos para uma questão de física 4?
Nesse problema vamos analisar uma rede de difração. Quando incidimos um feixe de luz com um único comprimento de onda (monocromático) em uma rede de difração, os máximos de interferência são analisados através de um espectro de raias que depende da distância entre as fendas, do tamanho delas e do comprimento de onda do feixe incidente.
Todavia, quando incidimos luz monocromática (com diferentes comprimentos de onda), cada comprimento de onda vai ter seu próprio espectro de raias e os máximos associados a cada comprimento de onda não vão coincidir. É sobre isso que esse problema trata!
Temos dois comprimentos de onda muito próximos, porém distintos e . Nós queremos analisar como a rede de difração separa as raias de cada um desses comprimentos!
Passo 2
No item (a), queremos saber qual deve ser a distância entre as fendas para que a separação angular entre as raias correspondentes aos máximos de primeira ordem () dos comprimentos de onda seja de . Para isso, usamos uma grandeza chamada dispersão :
Essa grandeza dá para gente a variação da separação angular com o comprimento de onda. Isolando , podemos escrever:
Nesse problema, radianos. Já é
Substituindo na equação para a distância entre as fendas:
Usei pois queremos analisar a separação dos máximos de primeira ordem. Fazendo as contas, achamos:
Ou ainda,
Passo 3
No item (b) queremos saber se fendas são suficientes para que possamos distinguir os máximos de segunda ordem referentes a cada comprimento de onda.
Para isso temos que usar o critério de Rayleigh! Essa discussão que eu vou fazer aqui já responde o item (c) que pergunta exatamente sobre isso...
A ideia básica é que para que possamos distinguir (resolver) dos máximos de comprimentos de onda distintos, o máximo central da figura de difração de um dos comprimentos de onda deve coincidir com o primeiro mínimo de difração do outro comprimento de onda. A seguir eu faço um desenho que ilustra a situação:
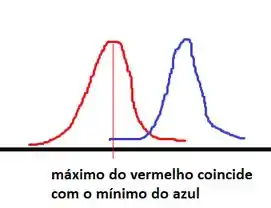
Com isso nós já respondemos o item (c)!
Passo 4
Para responder ao item (b), vamos considerar o desenho:
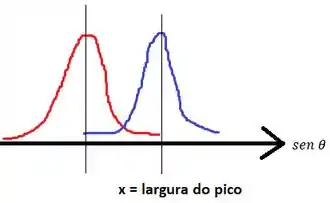
Essa distância que eu chamei de entre o máximo de um comprimento de onda e o máximo do outro (que coincide com o mínimo do primeiro) deve ser no mínimo igual a para que o critério de resolução de Rayleigh seja satisfeito:
Vamos lembrar também que essa distância deve ser um infinitesimal de , de modo que
Como estamos falando de ângulos pequenos, temos que . Portanto,
Portanto, o critério de resolução é
Mas vimos no passo 2 para resolver o item (a) que
Assim, o critério de Rayleigh pode ser escrito como
Simplificando e isolando :
Usando (estamos olhando para os máximos de segunda ordem), e , achamos que
Portanto, o número de fendas deve ser superior a 120. Logo, é suficiente para resolver e em máximos de segunda ordem!
Passo 5
Por fim, vamos ao item (d)!
Repare que a resolução já apareceu para gente no passo anterior. Podemos simplesmente escrever a relação
Ou ainda,
Observe que para distinguir as duas imagens, a resolução deve ser menor que o produto . Na situação limite, temos a igualdade!
Com isso, o que fizemos nos itens (b) e (c) servem de argumento para o item (d)!
E assim fechamos mais um problema 😊.
Resposta
é suficiente.