Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Reta Tangente à Interseção de Superfícies

Ver Teoria
Exercício 17123456789101112131415161819202122

Enunciado

Plano tangente e reta normal

Considere a curva C formada pela interseção do paraboloide 2 z = x 2 + y 2 com o elipsoide 2 x 2 + y 2 + z 2 = 4 . A reta tangente a C no ponto 1 , 1,1 intersecta o plano horizontal z = 0

  1. No ponto 3 , - 2,0
  2. No ponto 1,1 , 0
  3. No ponto 1 , - 1 / 2,0
  4. No ponto 1 / 3,2 , 0
  5. Em nenhum ponto, pois esta paralela a esse plano

Passo 1

Para achar a reta tangente a curva C , devemos achar um vetor v → tangente a essa curva.

Repara que o vetor normal ao paraboloide é perpendicular a esse vetor v → e o vetor normal ao elipsoide também é perpendicular a esse vetor v → . Isso acontece porque o vetor v → pertence tanto ao paraboloide quanto ao elipsoide, já que ele é tangente à curva formada pela interseção dos dois.

Então o vetor v → vai ser o produto vetorial entre os vetores normais ao paraboloide e ao elipsoide

Passo 2

Vamos primeiro achar o vetor normal n → , ao paraboloide. Primeiro fazemos

F x , y , z = x 2 + y 2 - 2 z

O vetor gradiente dessa função vai ser

∇ F = 2 x , 2 y , - 2

O vetor normal vai ser

n → = 2,2 , - 2

Passo 3

Vamos agora achar o vetor normal n → ' ao elipsoide. Primeiro fazemos

G x , y , z = 2 x 2 + y 2 + z 2 - 4

O vetor gradiente dessa função vai ser

∇ G = 4 x , 2 y , 2 z

O vetor normal vai ser

n → ' = 4,2 , 2

Passo 4

Vamos agora achar o vetor v →

v → = n → × n → '

v → = 2,2 , - 2 × 4,2 , 2

Vamos usar aquela parada de matriz para achar o vetor v →

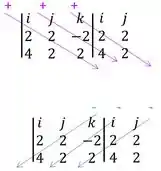
Então

v → = 4 i - 8 j + 4 k - 8 k + 4 i - 4 j

v = 8 i - 12 j - 4 k

Que vai ficar

v → = 8 , - 12 , - 4

A reta tangente vai ser

r t = 1,1 , 1 + t v →

r t = ( 1 + 8 t , 1 - 12 t , 1 - 4 t )

Passo 5

Se ele quer z = 0 vamos achar t para que isso aconteça

1 - 4 t = 0

t = 1 4

Substituindo esse valore de t vamos encontra

r 1 4 = 1 + 8 1 4 , 1 - 12 1 4 , 0

r 1 4 = 3 , - 2,0

O ponto é

3 , - 2,0

Resposta

Alternativa (a)

Exercícios de Livros Relacionados

Suponha que z = f ( x , y ) é uma função de classe C 1 , f 1,3 = - 1 , ∂ f ∂ x 1,3 = 4 e ∂ f ∂ y 1,3 = - 3 . Sabe-se que a curva σ t = t 2 , 4 t - 1 , z t , t ∈ R , está contida no gráfico da função z
Suponha que z = f ( x , y ) é uma função de classe C 1 , f 1,3 = - 1 , ∂ f ∂ x 1,3 = 4 e ∂ f ∂ y 1,3 = - 3 . Sabe-se que a curva σ t = t 2 , 4 t - 1 , z t , t ∈ R , está contida no gráfico da função z
Sejam S 1 e S 2 as superficies definidas por x 2 - y 2 + z 2 = 1 e x y + x z = 2 , respectivamente.Mostre que a reta tangente encontrada no item b ) é tangente à superficie de equação x y z - x 2 - 6
Sejam S 1 e S 2 as superficies definidas por x 2 - y 2 + z 2 = 1 e x y + x z = 2 , respectivamente.Determine equações da reta tangente à curva de interseção de S 1 e S 2 em ( 1,1 , 1 ) .
Nos Exercícios 13-18, encontre equações paramétricas para a reta tangente à curva de interseção das superfícies no ponto determinado S u p e r f i c i s : x + y 2 + z = 2 y = 1 Ponto: ( 1 / 2 , 1,1 /