Questão discursiva – UFJF - calculo 3 – lista de estudos – questão 6
Seja a a curva de interseção entre as superfícies e . Encontre uma parametrização para . Encontre a reta tangente a no ponto
Passo 1
Faaaaaala, galera... Tranquileba?? Mogli na área 😊. Bora responder Aí essa questão?
O problema nos pede para calcularmos dois passos: Dada uma curva formada por duas superfícies, achar a parametrização da curva, e além disso achar a reta tangente que tangencia essa curva. “Isso parece difícil, né?! Como fazer?”
Para a parametrização:
A parametrização de uma curva, que geralmente é bidimensional, tridimensional, ou n-dimensional é deixá-la somente em dependência de uma variável, por exemplo:
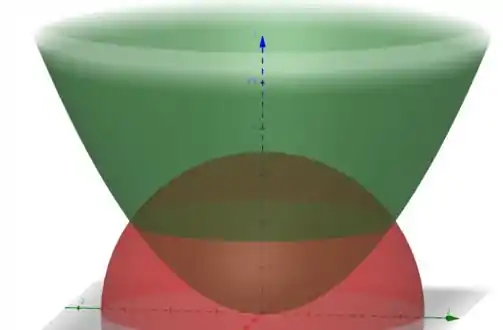
Agora veja que todas as componentes dependem de somente uma variável, que é . Quando isso é feito, chamamos que a função está parametrizada. Por exemplo, a superfície que é nos dada é:
E a curva de parametrização que vamos calcular é:
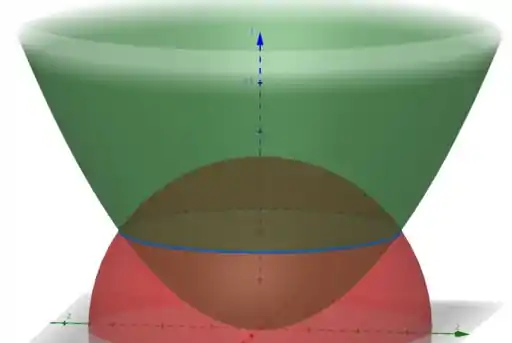
De forma que essa parametrização depende só de uma variável.
E para a reta tangente a curva:
A reta que tangencia a curva é dada pelo ponto somado à equação da curva no ponto, isto é:
Onde é o ângulo formado no ponto e é a derivada da parametrização.
Isso tudo parece confuso, mas fica mais fácil explicando... Cola junto!
Então já temos toda a ferramenta que vamos precisar. Vamos lá?
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Então para a parametrização:
Temos as duas superfícies:
Vamos igualar as duas equações e ver qual coordenada achamos? Podemos substituir na primeira equação e temos:
Então temos , vamos achar a raiz então dessa função
Aplicando Bhaskara:
Obtemos que:
Pelo gráfico sabemos que , logo .
Agora das outras equações temos que achar as parametrizações de e , temos então:
Mas , logo:
Podemos dividir ambos os lados por e:
Dessa equação podemos tirar uma identidade trigonométrica que é , né? Saca só, se fizermos e obteremos a parametrização completa, certo?
Geralmente as parametrizações são totais e levam, portanto,
Resumindo:
E agora que achamos a parametrização, vamos achar a reta tangente a esta curva no ponto ? Primeiro vamos achar o ângulo formado.
Passo 3
Temos a curva
No ponto temos por exemplo que , ou mesmo . Assim:
De forma que:
Agora que achamos o ângulo inicial formado pela parametrização e o ponto , vamos achar a a derivada da parametrização e nela?
Passo 4
Temos a curva :
Derivando em :
Agora aplicando
Obtemos então:
Logo a nossa reta tangente é:
E terminamos por aqui. Camarada. Obrigado por ter vindo até aqui comigo. Até a próxima!
Resposta
A parametrização:
E a nossa reta tangente é: