Exercícios Resolvidos de Análise da Multiplicação de Matrizes

Exercício 5 1 2 3 4 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

Enunciado

Uma montadora produz três modelos de veículos: , e . Neles podem ser instalados dois tipos de airbags: e . A matriz mostra a quantidade de unidades de airbags instaladas

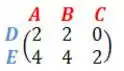
Numa determinada semana, foram produzidas as seguintes quantidades de veículos, dadas pela matriz :

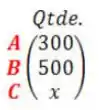
O produto da matriz pela matriz é .

Quantos veículos do modelo foram montados na semana?

a) 300

b) 200

c) 150

d) 0

e) 100

Passo 1

Ok, vimos que o produto entre a matriz pela matriz é igual a , ou seja:

E nós queremos encontrar o valor de , que é a quantidade de veículos no modelo belezinha? Pra isso vamos fazer a multiplicação das matrizes.

Passo 2

Multiplicando as matrizes:

Agora é só somar essas matrizes

Igualando os termos :

Ou seja, foram produzidas veículos do modelo . Logo, a alternativa correta é a letra B!!

Resposta

b) 200

Exercícios de Livros Relacionados

Resolva os sistemas seguintes achando as matrizes ampliadas linha reduzidas à forma escada e dando também seus pontos, os pontos das matrizes dos coeficientes e, se o sistema for possível, o grau de l

Explique por que a nulidade de uma matriz nunca é negativa.

Descreva todas as possíveis matrizes 2 X 2 , que estão na forma escada reduzida por linhas.

Faça o balanceamento das reações: N 2 O 5 → N O 2 + O 2 (decomposição térmica do N 2 O 5 )

Dados A = [[[1,-,3,2],[2,1,-,3],[4,-,3,-,1]]] , B = [[[1,4],[2,1],[1,-,2]] [[1,0],[1,1],[1,2]]] e C = [[[2,1],[3,-,2],[2,-,5]] [[-,1,-,2],[-,1,-,1],[-,1,0]]] mostre que A B = A C .