Uma bola esférica, condutora, sólida, em equilíbrio eletrostático, de raio , possui carga total . Tal bola é circundada por uma coroa esférica, isolante (de constante dielétrica ), de raios interno e externo , com uma carga total , uniformemente distribuída (pelo interior da coroa).

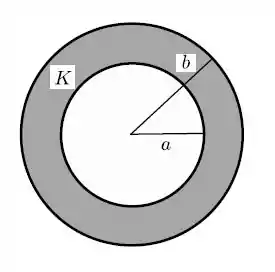
1. Calcule o vetor campo elétrico resultante (módulo, direção e sentido) nas três regiões: (I) ; (II) ; (III) .
2. Calcule o potencial elétrico resultante nas três regiões acima mencionadas, fazendo-o zero no infinito.

Além disso, pela configuração do campo, temos que o seu módulo é constante em toda , do que segue o fato:

Da última equação, segue que a integral de em toda é a área da Gaussiana. A área superficial de uma esfera é conhecida e é igual à:

Substituindo na Lei, temos:

Ainda pela configuração do campo, a simetria esférica nos dá que a componente do campo é radial:

Agora vamos de região em região. Para , se fecharmos uma gaussiana lá, temos que a carga interna é zero:

Pois num condutor em equilíbrio eletrostático as cargas ficam na superfície e o campo é zero. Vemos que as contas batem:

Para temos que a carga interna é tanto a da esfera, quanto a do pedaço da casca que estiver dentro da Gaussiana. Além disso, a Gaussiana está numa região de dielétrico, portanto dividimos a carga interna pelo fator . Você também pode argumentar que nessa região a permissividade muda e é igual à:

Acho que é melhor pro examinador essa justificativa. = ]

Acabou? Não, essa carga é uma variável que eu inventei e tem que ser calculado em função dos dados do problema.

Para achar , integramos a densidade de carga da casca isolante até os limites da Gaussiana:

Só que ele disse que a carga é uniformemente distribuída. Isto implica na densidade ser constante, portanto pode sair da integral:

A integral do diferencial de volume de uma esfera nada mais é do que o volume desta. Você poderia chegar à mesma conclusão se utilizasse aquela expressão () que nós mostramos no capítulo de densidade de carga. Mas enfim...

Lembrando que a densidade, por ser constante, é igual à carga total pelo volume total:

O volume total daquela casca nada mais é que o volume de uma esfera de raio menos o de uma esfera de raio :

Substituindo:

Substituindo láaaa em cima no Passo 4:

Arrumando né:

E temos o nosso campo para:

Agora vamos pra região final . Para esta, nós temos:

Portanto temos que a Lei de Gauss retorna, neste caso:

Agora vem uma questão super desagradável, tudo por causa daquele campo horrível entre e ... Utilizamos a fórmula do potencial:

Partindo do infinito pegando um caminho radial, temos, para a região :

Como o campo nesta região é nulo e o potencial do infinito também:

Agora vem a pica... Para a região partimos do ponto e fazemos:

Agora é “só” fazer essa integral aí! Partiu então... =’[

Arrumando:

Ah... Não deu tão feio quanto eu imaginava... Integrando:

Finalmente aplicamos os limites de integração:

Arrumamos para nossa própria saúde:

Finalmente, para a última região partimos de :

Só que o campo é nulo nessa região! Portanto:

Para achar o basta substituir na expressão do potencial anterior:

Logo, nessa região toda:

Chatinha né?