Na figura abaixo, dois capacitores de placas planas e paralelas e são ligadas em paralelo a uma bateria de . A área das placas dos capacitores é de e a distância entre as placas é de .
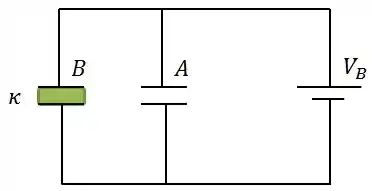
O dielétrico do capacitor é o ar, o do capacitor é um material de constante dielétrica igual a .
Determine o módulo do campo elétrico:
- No espaço entre as placas do capacitor ;
- No espaço entre as placas do capacitor ;
- Na placa de maior potencial do capacitor ;
- Na placa de maior potencial do capacitor ;
- Determine a densidade de cargas induzida na superfície superior do dielétrico do capacitor .
Determine a densidade de cargas livres
Passo 1
a) Determine o módulo do campo elétrico no espaço entre as placas do capacitor ;
Podemos calcular o campo elétrico entre as placas do capacitor através da relação:
Se os dois capacitores estão em paralelo, então a diferença de potencial entre os dois é a mesma, logo:
Agora sim!
Passo 2
b) Determine o módulo do campo elétrico no espaço entre as placas do capacitor ;
Opa! Calma, rapaz, cuidado pra não se enrolar com uma besteira aqui...
Lembra o que falamos no caso anterior? Se os dois capacitores estão em paralelo, os dois tem a mesma diferença de potencial... então o modo de calcular o campo elétrico é o mesmo para o caso anterior:
Passo 3
c) Determine a densidade de cargas livres na placa de maior potencial do capacitor ;
Primeiro vamos tentar usar algumas relações que já conhecemos pra simplificar a nossa vida.
Por definição, a densidade de cargas é dada por:
Em um capacitor de placas planas e paralelas:
Logo:
Como acabamos de ver:
Por fim:
Ou seja, só temos que pegar o valor do campo elétrico que acabamos de calcular e multiplicar pela permissividade do meio.
Passo 4
Para o capacitor , como o meio entre as placas do capacitor é o ar:
Agora ficou fácil.
Passo 5
d) Determine a densidade de cargas livres na placa de maior potencial do capacitor ;
Nesse caso, como o meio entre as placas é o dielétrico de constante , a permissividade passará a ser:
Portanto:
Passo 6
e) Determine a densidade de cargas induzida na superfície superior do dielétrico do capacitor .
Beleza! O que acontece aqui é o seguinte: A carga na superfície superior do dielétrico atrai a cargas negativas no dielétrico, induzindo uma carga a se localizar sobre a placa superior, conforme mostra a figura:
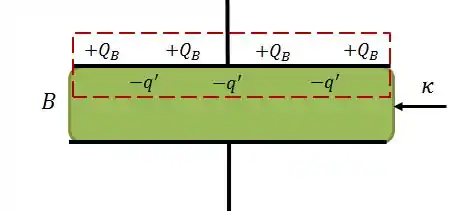
Usando a Lei de Gauss, temos que:
Pra deixar logo todo mundo aqui com cara de densidade de carga, vou dividir esses caras pela área .
Onde:
Portanto:
Como sabemos que é negativo:
Resposta
a.
b.
c.
d.
e.