Um capacitor carregado tem um campo elétrico inicial e uma diferença de potencial inicial entre suas placas.
Sem desliga-lo da bateria que o carregou, uma placa de dielétrico é inserida e preenche completamente o volume entre as placas, que produz um campo elétrico e uma diferença de potencial entre elas.
O par de afirmações que melhor representa as relações entre os campos elétricos e as diferenças de potencial antes e depois da inserção do dielétrico é:
; ;
; ;
; ;
; ;
; ;
Passo 1
Quando colocamos um dielétrico entre as placas do capacitor, temos geralmente duas casos que costumam ser cobrados em provas, que são:
- Carga constante;
- DDP constante;
O primeiro caso geralmente ocorre quando estamos analisando um capacitor isoladamente (mas o problema geralmente especifica isso), o segundo caso ocorre quando o capacitor está ligado a uma bateria, que é o nosso caso aqui.
Assim, a ideia é mais ou menos essa:
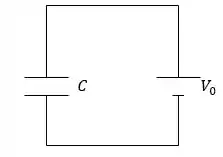
Se liga que, como não estamos desconectando o capacitor da bateria, ele sempre vai estar submetido à uma mesma ddp , logo:
Nesse caso, a única coisa que muda no capacitor após colocarmos o dielétrico será a carga.
Resposta
; ;