Considere um capacitor de placas paralelas cuja a área das placas é e cuja distância entre as placas é . Um dielétrico de constante dielétrica e espessura , com e , encontra-se centralizado entre as placas do capacitor. Suponha que a carga do capacitor seja , com a placa superior positiva e a placa inferior negativa, como ilustrado na figura abaixo. Despreze efeitos de borda.

(a) Sem precisar demonstrar, escreva a capacitância para os casos e .

(b) Sem precisar demonstrar, e para um valor de qualquer, indique: (i) o sinal das cargas induzidas nas superfícies superior e inferior do dielétrico; (ii) e a direção do campo elétrico em todas as regiões entre as placas do capacitor.

(c) Determine o módulo do campo elétrico dentro do dielétrico e entre o dielétrico e as placas do capacitor, para um valor de qualquer.

(d) Determine a capacitância do capacitor para um valor de qualquer.

(e) Encontre a carga induzida na superfície superior do dielétrico.

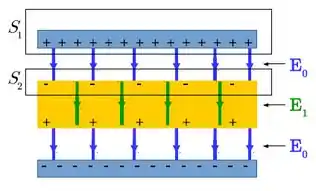
Bem, como a carga da placa superior do capacitor é positiva, a carga induzida na superfície superior do dielétrico será negativa. Da mesma forma, como a carga da placa inferior do capacitor é negativa, a carga induzida na superfície inferior do dielétrico será positiva.

O campo elétrico em todas as regiões é perpendicular às placas e aponta da placa positiva para a negativa.

A figura abaixo resume o que falamos aqui.

Entre o dielétrico e as placas, o campo elétrico pode ser calculado pela Lei de Gauss. Vamos utilizar a superfície gaussiana que mostramos na figura do item anterior.

Temos:

Já no interior do dielétrico, o campo elétrico é enfraquecido por um fator , ou seja,

Bem, a capacitância é dada por onde é a diferença de potencial entre as placas. Reescrevendo, temos

Vamos utilizamos a expressão para o cálculo da diferença de potencial elétrica, dada por:

onde os sinais de negativo e positivo nos limites inferior e superior da integral representam as placas negativa e positiva, respectivamente.

Sabemos os valores de e do último passo, certo? Vamos substituir na expressão do Passo 1 para obter:

Como

Agora, queremos encontrar a carga induzida na superfície superior do dielétrico. Para isso, utilizamos, novamente, a Lei de Gauss com a superfície gaussiana mostrada no item (b):

onde já estamos considerando carga interna como a carga induzida .

Isolando na expressão acima e substituindo os valores de e já calculamos, chegamos em: