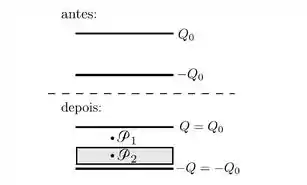
Considere um capacitor ideal de placas quadradas, planas e paralelas. Mantendo-se a carga de cada placa constante, uma chapa espessa de isolante, é inserida na região entre as placas do capacitor original. Sendo o módulo do campo elétrico entre as placas do capacitor original, e (i = 1, 2) os módulos do campo elétrico, nos pontos (i = 1, 2), após a introdução do
isolante, o que pode ser afirmado sobre tais módulos?
(a) .
(b)
(c) .
(d) .
(e) .
(f) .
(g) .
(h) .
Passo 1
Primeiramente, vamos tentar visualizar melhor o que está acontecendo.
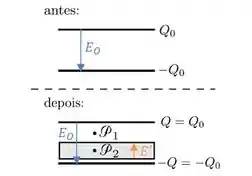
Ao inserir o dielétrico, um campo elétrico é induzido () aparece no dielétrico, devido a polarização das cargas.
Passo 2
Podemos resolver esse exercício fazendo a soma dos vetores de campo elétrico presentes em cada ponto.
Como a carga nas placas do capacitor não muda, o campo também aparece depois que o dielétrico é inserido.
No ponto só há o campo original e portanto o campo elétrico nesse ponto é o mesmo que o de antes de inserir o dielétrico.
Portanto:
No ponto temos o vetor do campo original e também o vetor do campo induzido .
O campo elétrico resultante vai ser a soma desses vetores, lembrando que eles têm sentidos contrários!
Temos:
Considerando apenas os módulos, temos:
Portanto, como esperado, o dielétrico diminuiu o campo elétrico no capacitor, mas nesse caso apenas na região de
Passo 3
Juntando tudo temos:
A alternativa correta é a letra (g)
Resposta
(g) .