Considere um capacitor esférico de raio interno e raio externo com uma carga , conforme mostra a figura abaixo.
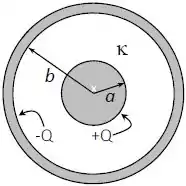
A região entre as placas do capacitor é preenchida por um dielétrico de constante dielétrica .
Use a Lei de Gauss em meios dielétricos para mostrar que o módulo do campo elétrico entre as placas do capacitor é
Calcule a capacitância deste capacitor.
Justificando claramente sua resposta, determine a carga induzida na superfície interna do dielétrico, ou seja, em .
Passo 1
Use a Lei de Gauss em meios dielétricos para mostrar que o módulo do campo elétrico entre as placas do capacitor é
Em um meio dielétrico a permissividade passa a ser dada por:
A Lei de Gauss é dada por:
Aplicando a Lei de Gauss na região esférica entre as duas superfícies, teremos:
Passo 2
Calcule a capacitância deste capacitor.
Como já temos o campo elétrico, o próximo passo para calcular a capacitância é o cálculo do potencial elétrico, dado por:
A capacitância é dada por:
Onde:
Finalmente:
Passo 3
Justificando claramente sua resposta, determine a carga induzida na superfície interna do dielétrico, ou seja, em .
Voltando à Lei de Gauss. A constante dielétrica aparece em decorrência de cargas induzidas no interior do dielétrico.
Assim, junto à superfície de raio e carga , será induzida uma carga .
Logo, aplicando novamente a Lei de Gauss, temos:
Reorganizando isso, teremos:
Resposta