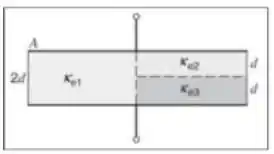
Considere um capacitor de placas paralelas preenchido por três dielétricos distintos , conforme demonstrado na figura abaixo. Sabendo que a distância entre as placas é e a área delas é , calcule a capacitância desse capacitor. Considere
Passo 1
Oi, tudo bem?
Essa questão parece complicada, mas vou ajudar você aqui! Vamos lá? O problema nos deu um capacitor de placas paralelas preenchido com três dielétricos diferentes. E perguntou qual é o valor da capacitância equivalente nesse caso.
Nesse tipo de questão, o essencial é que você consiga desenhar esse capacitor como uma combinação de capacitores (em paralelo e em série) e ir calculando a equivalência desse aos poucos.
Então vamos começar redesenhando esse cara! Bom, primeiro vou inverter! Assim você vai conseguir ver melhor, saca só:
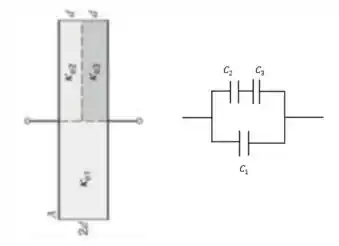
Ao virar esse capacitor de pé fica mais fácil enxergar que temos dois capacitores em série em cima (com as capacitâncias e ) e que estão em paralelo com o capacitor de baixo (com capacitância )
Beleza?
Então o que precisamos calcular é a capacitância equivalente desse capacitor!
Passo 2
A capacitância equivalente de dois capacitores ligados em série é a soma dos inversos:
Aqui , então podemos calcular a capacitância dessa parte:
Então a capacitância equivalente é
Beleza?
Tudo bem até aqui?

Passo 3
Com a capacitância calculada, podemos redesenhar o capacitor trocando e por um único capacitor :
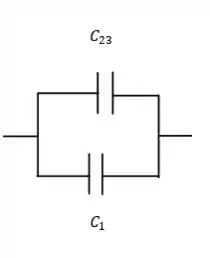
O equivalente da capacitância quando ligada em paralelo é a soma simples das capacitâncias! Então a capacitância equivalente desse capacitor é:
Passo 4
Um capacitor de placas paralelas tem capacitância igual a
Como temos um dielétrico , então a capacitância é
Embora a área das placas sejam as mesmas, as distâncias entre as placas não são. Vamos voltar ao desenho original e verificar isso:
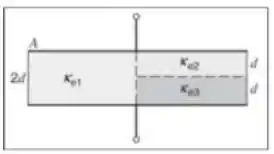
A distância entre as placas para o capacitor é , já para os outros dois capacitores é . Então o que precisamos fazer agora é calcular cada capacitância em função de e para depois substituir na expressão para a capacitância que encontramos no passo anterior! Beleza?
Passo 5
Começando pela capacitância : a distância entre as placas é e tem área
Lembrando que .
Agora para a capacitância de :
Lá do passo 2, a capacitância equivalente é
As distancias entre as placas é e cada um tem seu dielétrico e .
Assim as capacitâncias são
E substituindo na expressão da capacitância equivalente
Beleza?

Passo 6
E agora a capacitância equivalente:
E lembrando que , então a expressão em termos dos parâmetros geométricos das placas é
Passo 7
O problema nos deu valores para os dielétricos, para a distância entre as placas e para a área. E perguntou o valor da capacitância. Agora é só substituir:
A capacitância equivalente:

Espero ter ajudado! Até a próxima!