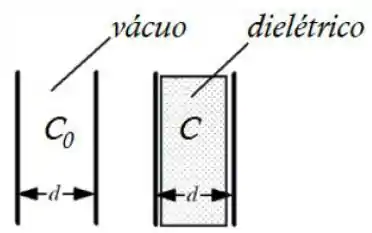
Um capacitor de capacitância no vácuo é conectado a uma bateria que sustenta uma tensão adquirindo, portanto, uma carga . A seguir, o capacitor é desconectado da bateria e um dielétrico de constante é inserido entre suas placas. Os novos valores da capacitância , da carga e da tensão entre as placas serão:

Precisamos de uma informação muito importante aqui no caso de dielétricos: a nova capacitância de um capacitor aumenta quando colocamos um dielétrico dentro dele:

Quando ligamos a bateria de tensão , o capacitor é carregado e fica com carga . Se a bateria é retirada, a carga sobre as placas do capacitor não muda, por isso, .

Substituindo em , teremos o seguinte:

que simplificada, tem como resultado:

Resumindo, depois de a bateria ser desligada e o dielétrico ser colocado entre as placas, o que temos é o seguinte: