Uma placa dielétrica de espessura e constante dielétrica é introduzida entre as placas de um capacitor plano, as quais estão separadas pela distância . Cada placa possui área igual a . Mostre que a capacitância é dada por:
Passo 1
Vamos olhar para a representação da figura abaixo.
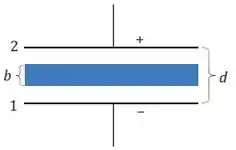
Sem considerarmos a presença do dielétrico, a capacitância seria dada por:
Logo, a carga acumulada no capacitor pode ser escrita por:
onde é a tensão antes de introduzir o dielétrico.
Passo 2
Considerando agora que o dielétrico foi colocado entre as placas, precisamos encontrar um novo valor de tensão, já que a carga irá permanecer constante.
Vamos usar a seguinte expressão:
Aqui, integramos da placa até a placa , como na figura. Temos:
onde é o módulo do campo elétrico antes da presença do dielétrico e é o módulo do campo elétrico depois da presença do dielétrico.
Passo 3
Bem, podemos calcular o valor de como:
Substituindo na equação de :
Passo 4
Da definição de capacitância, temos que:
Substituindo os valores de e encontrados:
Como a relação entre a tensão inicial e o módulo do campo inicial é dada por:
teremos que:
Usando a expressão calculada para no passo 1, chegamos a:
Resposta
Ei, a resposta está no passo a passo :)