Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Difração por Duas Fendas Simples

Ver Teoria
Exercício 161234567891011121314151718192021222324252627282930313233343536

Enunciado

(I) Considere um conjunto de duas fendas de largura l , espaçadas por uma distância de 5 l . Sobre estas duas fendas incide uma onda plana monocromática, cujo comprimento de onda é igual a l / 2 , conforme a figura.

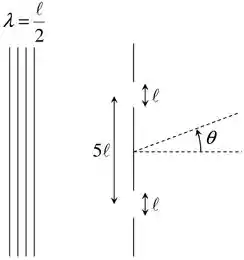
  1. Para quais valores do ângulo de observação θ , indicado na figura, serão observados os dois primeiros mínimos de difração adjacentes ao máximo central?
  2. Considere a região angular 0 ≤ θ ≤ 30 ° . Qual é o número de mínimos de interferência nesta região?

Passo 1

Sabemos que os mínimos de difração ocorrem quando

a s e n θ = n λ

com

n =   ± 1 ,   ± 2 ,   ± 3 ,   …

Então os nossos dois primeiros mínimos de difração vão aparecer quando n = ± 1 . Substituindo na equação anterior e sabendo que a largura da fenda é a = l e que o comprimento de onda é λ = l / 2 , temos:

s e n θ = n λ a = ± l / 2 l = ± 1 2

Agora é só tirar o arcoseno de 1 / 2 e pronto!

θ 1 = ± 30 °

Passo 2

Sabemos que os mínimos de interferência são dados pela condição

d s e n θ = n + 1 2 λ

com

n =   0 , ± 1 ,   ± 2 ,   ± 3 ,   …

Para satisfazer essa condição o seno do ângulo deve também obedecer

0 ° ≤ θ ≤ 30 ° →     s e n 0 ° ≤ s e n θ ≤ s e n 30 ° → 0 ≤ s e n θ ≤ 1 / 2

Por outro lado a condição para o mínimo de interferência usando λ = l / 2 e d = 5 l (dados no enunciado), temos

s e n θ = n + 1 2 λ d = n + 1 2 l / 2 5 l = n + 1 2 1 10

Agora combinando as duas condições

0 ≤ n + 1 2 1 10 ≤ 1 2

- 1 2 ≤ n ≤ 9 2

Os únicos inteiros (já que n só pode ser inteiro) possíveis são

n = 0,1 , 2,3 , 4

Logo há 5 mínimos nessa região

Resposta

  1. θ 1 = ± 30 °
  2. há 5 mínimos nessa região

Exercícios de Livros Relacionados

Quando uma das fendas de um sistema de dupla fenda é coberto com uma placa fina de mica ( n = 1,58 ), o ponto central da tela de observação passa a ser ocupado pela sétima franja lateral clara ( m = 7
A Fig. 35-39 mostra duas fontes luminosas isotrópicas, S 1 e S 2 , que emite em fase com um comprimento de onda de 400n m e mesma amplitude. Um detector P é colocado no eixo x , que passa pela fonte S
A luz solar é usada em um experimento de dupla fenda. O máximo de quarta ordem para um comprimento de onda de 450n m é observado para um ângulo θ = 90 ° . Assim, está no limite para ser excluído da fi
Um padrao de interferencia de fenda duplaeformado usando luz de laser monocromatica com comprimento de onda de 640 nm.No segundo maximo a partir do maximo central,qual ea diferenca de caminho optico e
Um padrão de interferência-difração de fenda dupla do tipo Fraunhofer é observado usando luz com comprimento de onda 700 nm. As fendas têm largura de 0,010 mm e estão separadas por 0,20 mm. Quantas fr