Em um laboratório de óptica, deseja-se obter um padrão de intensidade com 9 franjas brilhantes, exatamente, dentro do máximo central da difração. Utiliza-se nessa tarefa um anteparo com duas fendas idênticas, separadas pela distância de 15mm, com luz de comprimento de onda de 600nm. A distância entre a tela de observação e o anteparo é de 10m. O padrão de intensidade desejado é obtido com fendas de qual largura:
(a)
(b)
(c)
(d)
(e)
(f) É impossível obter tal padrão de intensidade com o comprimento de onda utilizado.
Passo 1
O nosso objetivo é determinar o tamanho das nossas fendas para que dentro de um máximo central de difração caibam 9 franjas de interferências, para isso teremos que lembrar de algumas fórmulas e relações.
Nesse caso temos que analisar o seguinte, precisamos relembrar como calcular o tamanho do máximo central de difração. Para isso precisamos lembrar onde ele termina. Nesse caso o mínimo de difração é dado pela fórmula,
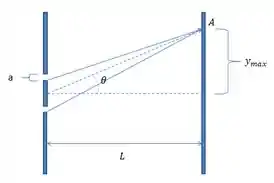
E pelo desenho vemos o seguinte
Podemos aproximar para ângulos pequenos o seguinte
Logo podemos fazer a seguinte substituição
Substituindo teremos que
Mas lembre-se que queremos o tamanho do máximo central, logo, queremos para o valor de
Passo 2
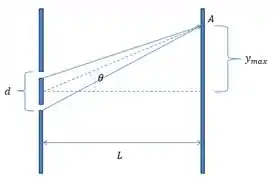
Agora pensa no seguinte, se temos o valor do tamanho do máximo central precisamos fazer caber nesse espaço as 9 franjas claras, mas tome o seguinte cuidado, perceba que calculamos apenas para a metade superior, ou seja, sabemos que tem 4 franjas pra cima, 1 no meio e 4 franjas pra baixo, fechando então as nossas 9 franjas, logo, no nosso calculo para máximos de interferências não usaremos m=9, mas m=5, pois pensa no seguinte, queremos as 4 franjas de cima mais a franja do meio, totalizando 5 no .
Olhando o desenho temos que
Fazendo o mesmo processo feito para o caso anterior teremos
Substituindo teremos
Passo 3
Como queremos que todas as franjas de interferências caibam no máximo central de difração basta igualar os
Isolando o valor de teremos
Como o valor de d=15 teremos
Resposta
(D)