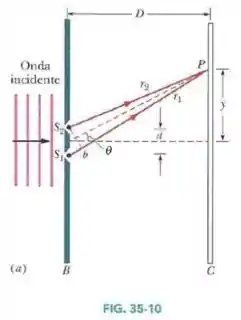
Um feixe luminoso monocromático incide perpendicularmente em um sistema de dupla fenda como o da Fig. 35-10. As fendas têm de largura e a distância entre as fendas é .
Quantas franjas claras completas aparecem entre os dois mínimos de primeira ordem da figura de difração?
Passo 1
Vamos fazer esse exercício de duas formas, para treinarmos: A primeira é passo a passo, e a segunda é usando uma dica que diminui muito todo o trabalho (pois ele está todo dentro da dica).
Primeiro nós precisamos saber a distância desses dois mínimos até o centro da figura de difração. Usamos então a condição de mínimos de difração:
Onde é a largura das fendas e é o comprimento de onda da luz. Sendo os dois primeiros mínimos de difração, . Então, o ângulo de cada um é dado por:
Passo 2
Agora, precisamos achar o máximo de interferência com a maior distância do máximo central tal que ela ainda seja menor que a distância dos primeiros mínimos.
Condição de máximos de interferência:
Onde é a distância entre as fendas e é o comprimento de onda da luz. Vamos dizer que o máximo que procuramos é de ordem . Então, seu ângulo é dado por:
Passo 3
Como comentamos antes, o ângulo do máximo de ordem tem que ser menor que o do primeiro mínimo de difração (estamos olhando apenas para o mínimo onde por enquanto)
Logo:
E temos 6 máximos de interferência de um dos lados do máximo central. Se fizermos o mesmo para o outro lado, obteríamos a mesma coisa, porém com . Isso é porque a figura é simétrica.
Logo, temos 12 máximos do lado do máximo central, somando 13 máximos no total (seis de cada lado mais o central).
Passo 4
A forma mais rápida de fazer é pular as etapas de forma consciente.
Todas as etapas que fizemos é o mesmo que procuramos o maior tal que:
Onde é a distância entre as fendas e é a largura das fendas. Substituindo, teríamos de forma direta:
Porém, temos que lembrar que essa desigualdade é para apenas um dos dois lados do máximo central. Então, o número de máximos entre os dois primeiros mínimos de difração seria duas vezes esse valor acrescido de um, representando o próprio máximo central.
Resposta
Entre os dois mínimos de primeira ordem da figura de difração aparecem 13 franjas claras.