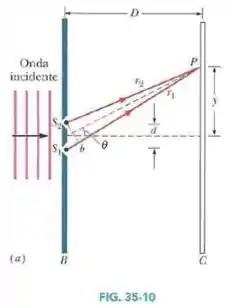
No experimento de interferência de dupla fenda da Fig. 35-10, a largura das fendas é , a distância entre as fendas é , o comprimento de onda é e a tela de observação está a uma distância de .
Seja a intensidade no ponto da tela, situado a uma altura .
- Determine a razão entre e a intensidade no centro da tela.
- Determine a posição de na figura de interferência, especificando o máximo ou o mínimo no qual o ponto se encontra ou o máximo e o mínimo entre os quais o ponto se encontra.
- Determine a posição de na figura de difração, especificando o mínimo no qual o ponto se encontra ou os dois mínimos entre os quais o ponto se encontra.
Passo 1
Letra a)
O nosso primeiro passo é encontrar o ângulo entre o centro da figura e o ponto .
Sabemos que a distância do centro ao ponto é de e a distância das fendas ao anteparo é de .
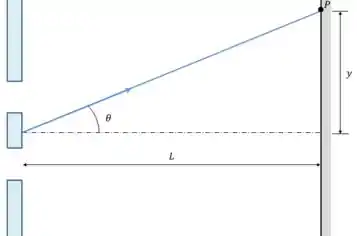
A tangente do ângulo vai ser a razão desses dois valores:
Passo 2
A razão entre e vai ser:
Onde:
Nessas fórmulas, é a largura das fendas, é a distância entre as fendas e é o comprimento de onda da luz incidente.
Usando o ângulo que encontramos antes:
Juntando todos os resultados:
Passo 3
Letra b)
As condições dos máximos de interferência são:
Enquanto as dos mínimos:
O ângulo do nosso ponto é cujo seno vale:
Em múltiplos de , temos:
Ou seja, está entre o mínimo com (sexto mínimo) e o máximo com (sétimo máximo.
Passo 4
Letra c)
As condições dos mínimos de difração são:
O ângulo do nosso ponto é cujo seno vale:
Em múltiplos de , temos:
Ou seja, está entre o mínimo com (terceiro mínimo) e o mínimo com (quarto mínimo).
Resposta
Letra a)
Letra b)
O ponto está entre o sexto mínimo e o sétimo máximo de interferência.
Letra c)
O ponto está entre o terceiro mínimo e o quarto mínimo de difração.