Um fio bem fino é colocado na abertura de um apontador laser. A luz emitida tem comprimento de onda de 532 nm. A tela de observação está situada a 2,0 m de distância do apontador. Observa-se franjas de difração com distância de 16,4 cm entre mínimos sucessivos. Determine a espessura do fio.
Passo 1
Nessa questão sabemos que se trata de uma interferência em fenda simples, ou seja, que não é considerada uma fenda pontual mas que apresente um tamanho considerável comparado com as fendas pontuais.
Sabemos que nessa caso um mínimo de difração pode ser dado por
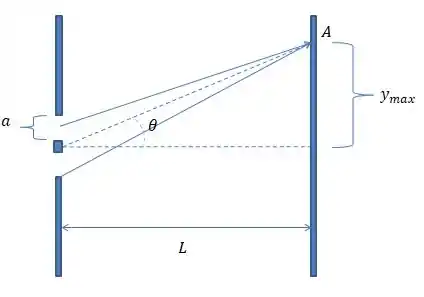
Mas observe a figura
Sabemos que por essa figura podemos fazer a seguinte aproximação quando temos pequenos ângulos
Se substituirmos na nossa equação principal teremos
Como se trata de um fio muito fino, iremos aproximar a espessura do fio para espessura da fenda, dessa forma queremos o valor de a, então, vamos isolar esse valor na nossa equação.
Passo 2
Agora que já sabemos a nossa equação basta substituir os valores
E agora a duvida que pode surgir é em relação ao valor de n, porém como ele disse que o valor de simboliza a distância ente dois mínimos consecutivos, significa que o valor de só poderia ser 1
Logo
Substituindo esses valores teremos