Um dispositivo de difração por duas fendas, supostas iguais, é iluminado com um laser de comprimento de onda λ = 630 nm e produz uma imagem projetada sobre uma tela de observação, distante L = 1,0 m da tela das fendas. O máximo de interferência de ordem 1 dentro da envoltória central de difração se forma em = 2,0 x m. O primeiro mínimo de difração se forma em = 1,0 cm. Determine:
(a ) A distância entre os centros das fendas.
(b ) A largura de uma fenda.
(c ) O número de máximos de interferência completos na envoltória central de difração.
(d ) A razão entre as intensidades da primeira franja brilhante (m = 1) e a franja central.
Passo 1
Vamos primeiro analisar o exercício através de uma imagem
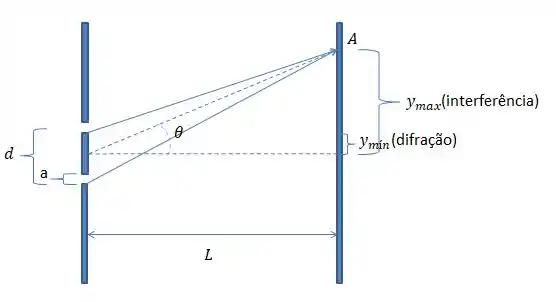
O primeiro item nos pede para determinar a distancia d entre o centro das fendas, como ele quer o valor de d temos que relacionar o nosso exercício com a fórmula de interferência.
Sabemos que um máximo de interferência ocorre quando podemos usar a fórmula
Em que m= 0,
Mas lembra que os ângulos que usamos são pequenos ?
Com isso podemos usar a relação que diz
Essa relação só vale para ângulos pequenos.
Passo 2
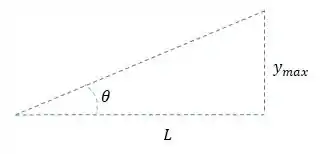
Mas pelo exemplo vemos que
E sabemos que a nossa fórmula para franjas claras é
E que para ângulos pequenos vale a relação
Substituindo teremos que
Com isso concluímos que o nosso vai ser dado pela fórmula
Passo 3
Com a fórmula em mãos temos apenas que substituir os valores, vamos lembrar quanto cada um vale.
substituindo teremos
Passo 4
Agora no item b iremos analisar os mínimos de difração.
Mas o que o exercício quer?
O exercício quer que definamos o tamanho, ou seja, largura do das fendas, mas lembre-se que para fendas simples, a fórmula que nos da os mínimos, e aqui vale uma observação, pois para interferência a fórmula dava máximos, mas para fendas simples ela nós dará mínimos e a fórmula é a seguinte.
Em que m=
Agora pensa no seguinte, se no exercício já nos dá a distancia do primeiro mínimo de difração, basta relacionar essa fórmula com a distancia do mínimo e assim achar o valor de , vamos fazer isso então.
Passo 5
De novo podemos considerar que é muito pequeno, logo
E pelo desenho que fizemos podemos considerar pelo triangulo que
Substituindo isso na nossa equação para franjas simples, teremos que
E isolando o valor de encontraremos
E os nossos valores são
Passo 6
Nesse item queremos saber quantos máximos de interferência existem no nosso máximo de difração, mas pensa no seguinte, nos sabemos que as posições dos nosso mínimos de difração são dados pela fórmula
Apenas para diferenciar chamaremos o m de difração de n, logo teremos
E a posição dos nossos máximos de interferência são dados pela fórmula
Como queremos que todas as franjas de interferências caibam no máximo central de difração basta igualar os
Como queremos o numero de máximos de interferências devemos pensar no seguinte, quantos máximos cabem na difração até chegar o primeiro mínimo de difração, ou seja, quando n=1.
Fazendo as substituições, teremos
Mas aqui temos que tomar o seguinte cuidado, para m=5 temos um máximo de interferência exatamente em cima do nosso mínimo de difração, ou seja, esse ponto é descartado não sendo considerado no máximo central de difração, o que nos dá 4 máximos de interferências acima do máximo central, mas lembre-se que abaixo do máximo central de interferência os mesmos valores se repetem, ou seja, temos 4 máximos de interferência acima do centro, 4 abaixo do centro e 1 que está no próprio centro, e todos esses valores estão dentro do máximo de difração central, ou seja, o total de máximos de interferências no máximo central serão
Passo 7
Por fim, o ultimo item quer que façamos a razão entre o intensidade da primeira franja brilhante e a franja central, para isso devemos lembrar que a fórmula da intensidade nesse caso é dado por.
Mas aqui temos uma vantagem, como se trata de máximos de interferência, o fator pode ser considerado igual a 1, dessa forma a nossa fórmula passa a ser
Agora precisamos lembrar que o nosso se trata da diferença de fase dada por caminho percorrido.
A fórmula é bem simples
Mas como podemos simplificar essa equação? Lembra da fórmula de máximos de interferência? Ela é dada por
Como queremos saber a intensidade no ponto em que m=1, ou seja, primeiro máximo de interferência após o central, teremos que
Dessa forma podemos simplificar nossa equação de diferença de fase da seguinte forma
Como já temos o valores de e , basta substituir
Agora que temos a diferença de fase, basta substituir na fórmula da intensidade
Agora que temos o valor basta saber o seguinte
Fazendo essa razão teremos
Resposta
a)
b)
c)
d)