04) Pedro e Paulo decidem se encontrar em um certo local. Se cada um deles chega a esse local independentemente em um instante uniformemente distribuído entre meio-dia e uma hora da tarde, qual a probabilidade de que o primeiro a chegar espere mais do que 20 minutos?
A)
B)
C)
D)
E)
Passo 1
Faaaaala galera, como vocês estão?
Aqui temos uma questão de probabilidade que fala sobre o encontro de dois amigos, que combinaram de chegar em um local entre meio-dia e uma hora, mas ninguém quer esperar mais do que minutos. Precisamos descobrir qual a probabilidade disso acontecer, ou seja, do primeiro a chegar esperar mais do que minutos.
Tem uma palavrinha-chave no enunciado que vai nos dar todo o caminho de como resolver essa questão, você consegue achar ela?

É o trechinho que diz “...instante uniformemente distribuído”. Ou seja, o tempo de espera nesse exercício é uma variável aleatória da distribuição uniforme. Isso é fundamental, por ser uniforme cada instante de tempo entre e é equiprovável. Então, bora relembrar a sua função de densidade:
Massa! Nesse caso, como os amigos chegam entre meio-dia e uma hora da tarde, podemos considerar e .
Passo 2
Então, já entendemos o que está acontecendo na questão, mas como é que resolve ela?
Nesse caso, se tentássemos calcular a probabilidade usando a função de densidade teríamos algumas dificuldades. Isso porque, não temos apenas uma variável representando o tempo, na realidade o horário que Pedro e que Paulo chegam representam, cada um, uma variável. Isso dificulta um bocado a nossa vida.
Maaaas, trago boas novas, tem uma forma de calcular essa probabilidade sem nem tocar em integral, usando apenas o recurso gráfico! Vem comigo!
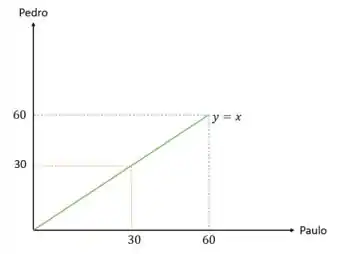
Esse gráfico representa, em e , os instantes que Paulo e Pedro podem chegar, respectivamente. Cada um deles pode chegar entre e minutos. Inicialmente traçamos a reta que representa os pontos nos quais os amigos chegam no mesmo horário.
Imagina agora que Paulo é o amigo que chega atrasado, então se ele respeitar os minutos de tolerância temos as seguintes possibilidades:
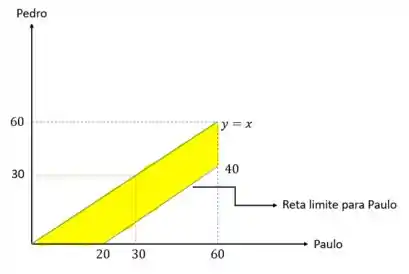
Nota que nesse gráfico, para cada valor possível de chegada de Pedro (reta ), temos um correspondente valor limite para chegada de Paulo (Reta limite). Qualquer valor entre essas duas retas (região em amarelo) respeita a tolerância de minutos.
Beleza, mas e se quem estiver atrasado for Pedro? Bora desenhar o gráfico análogo também.
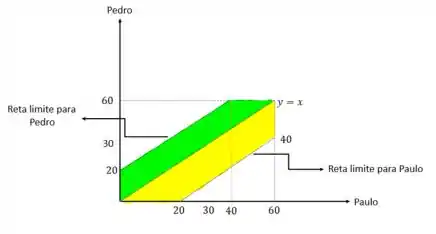
Assim como fizemos anteriormente, traçamos também a reta limite para Pedro. Toda essa região em verde compreende os possíveis instantes em que Pedro pode chegar atrasado respeitando a tolerância de 20 minutos em relação a Paulo.
Passo 3
Beleza, fizemos esses gráficos, mas como que isso nos ajuda?
É que, já que a distribuição é uniforme, cada par são equiprováveis. Assim, a probabilidade pode ser calculada através da razão de áreas desse gráfico.
Nesse caso, queremos a probabilidade dos amigos chegarem mais de minutos atrasados um em relação ao outro.
Podemos usar a complementaridade e calcular, inicialmente, a probabilidade deles respeitarem a tolerância de minutos. Assim:
Pois, como mostramos anteriormente, a área verde e amarelo correspondem ao respeito de tolerância do atraso.
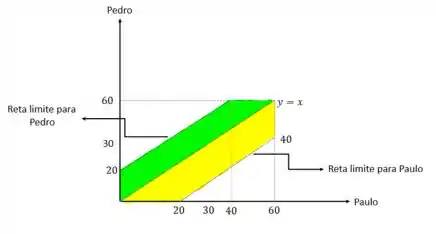
Temos:
Já a , é o retângulo completo. Daí:
Portanto, temos:
Porém, como a probabilidade que queremos é a complementar a essa, vem que:
Prontinho! Gostaram da sacada? Essa ideia minimiza bastante as contas.
Até a próxima, galera! 😉
Resposta
Letra D: