Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Distribuição Uniforme

Ver Teoria
Exercício 111234567891012131415161718192021

Enunciado

TAREFA da aula-3- Probabilidade e Estatística – Questão 1

O salário (em milhares de reais) dos funcionários numa empresa pode ser modelado por uma variável contínua X com a seguinte densidade:

f x = c x 2 ,     s e   2 ≤ x ≤ 8

a) Ache a constante c que faz de f ( x ) uma função de densidade de probabilidade. Plote a função f ( x ) .

b) Encontre a função de distribuição de densidade de probabilidade de X para qualquer número real x . Plote a função F ( x ) .

c) Ache o ponto m entre 2 e 8 tal que P r ( X ≤ m )   =   0.50 . Este ponto é a mediana de X , ou seja, o salário mediano dos funcionários desta empresa.

Passo 1

E aí, galerinha!

Tarefinha 3, agora!

a) Bom! Nessa primeira letra, a questão dá a função f ( x ) , igual à...

f x = c x 2

Com 2     x     8 e pede pra gente determinar o c que faz de f ( x ) uma função de densidade de probabilidade.

Se liga! O requisito básico pra que uma função seja de densidade de probabilidade é preciso que...

∫ - ∞ ∞ f x d x = 1

Como nosso x vai de 2 até 8 , então...

∫ - ∞ ∞ f x d x = ∫ 2 8 c x 2 d x = 1

Resolvendo a integral...

∫ 2 8 c x 2 d x = 1

∫ 2 8 c x 2 d x = - c x 2 8 = - c 8 - - c 2 = 1

- c 8 + c 2 = 1

c 1 2 - 1 8 = 1

3 8 c = 1

c = 8 3

c = 2.6667

Pronto! Esse é o valor de c para a função ser de densidade de probabilidade.

Passo 2

Achado c , a nossa função vai então, ser dada por...

f x = 8 3 x 2 ,   s e   2 ≤ x ≤ 8

Plotando ela em um gráfico, temos que...

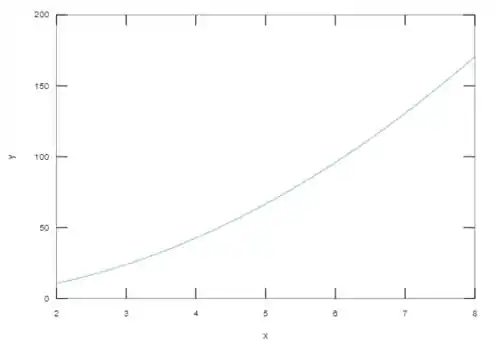
Passo 3

b) Bom! Como a nossa função   c / x 2 vai de 2 até 8 , podemos escrever f ( x ) assim...

f x = 0 ,       s e   x < 2 c x 2 ,   s e   2 ≤ x ≤ 8 0 ,   s e   x > 8 = 0 ,       s e   x < 2 8 3 x 2 ,   s e   2 ≤ x ≤ 8 0 ,   s e   x > 8

Nesse item aqui, a gente tem que encontrar a função de distribuição de densidade de probabilidade de X para qualquer número real x . Na prática, só o que a gente tem que fazer é integrar as outras funções de f ( x ) .

A integral de c / x 2 , por exemplo, vale...

∫ c x 2 d x = - c x

Sendo assim, temos que...

F X = 0 ,       s e   x < 2 - c x ,   s e   2 ≤ x ≤ 8 0 ,   s e   x > 8

Com c = 8 / 3 :

F X = 0 ,       s e   x < 2 - 8 3 x ,   s e   2 ≤ x ≤ 8 0 ,   s e   x > 8

Plotando o gráfico, temos que...

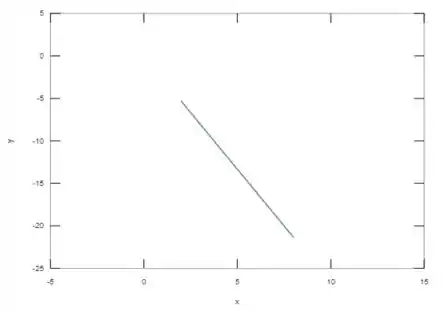
Passo 4

c) Pra finalizar, a gente tem que achar o ponto m entre 2 e 8 tal que P r ( X     m )   =   0.50

Se liga! A gente tem que...

f x = 8 3 x 2 ,   s e   2 ≤ x ≤ 8

Pra gente achar o ponto m entre 2 e 8 é só usar a integral abaixo

∫ 2 m 8 3 x 2 d x

E o resultado dessa integral tem que ser igual à 0.5 ;

∫ 2 m 8 3 x 2 d x = 0.5

∫ 2 m 8 3 x 2 d x = - 8 3 x 2 m = 0.5

- 8 3 m - - 8 3 ⋅ 2 = 0.5

- 8 3 m + 8 6 = 0.5

8 3 m = 8 6 - 1 2

8 3 m = 8 6 - 3 6

8 3 m = 5 6

15 m = 48

m = 3.2

Pronto! Essa é a mediana dos salários da empresa!

Os caras aí ganham em torno de 3.2 mil reais!

Resposta

a)

c = 8 3

b)

F X = 0 ,       s e   x < 2 - 8 3 x ,   s e   2 ≤ x ≤ 8 0 ,   s e   x > 8

c)

m = 3.2

Exercícios de Livros Relacionados

Erro de medida, que é distribuído contínua e uniformemente de -3 a +3 milivolts, é adicionado ao valor verdadeiro da tensão de um circuito. Então, a medida é arredondada para o milivolt mais próximo,
A espessura de um flange em um componente de espaçonave é uniformemente distribuída entre 0.95 e 1.05 milímetros.Determine a função de distribuição cumulativa da espessura do flange.Determine a propor
Suponha que a variável aleatória discreta X tome os valores 1, 2 e 3 com igual probabilidade. Ache a distribuição de probabilidade de Y = 2X + 3.
Com referência ao Ex. 4.10, calcule P(X = 2), se n = 4 e, para n arbitrário, verifique P(X = n-1) = P (exatamente uma tentativa mal sucedida) é igual a 1 n + 1 ∑ 1 i
Um experimento consiste em tentativas independentes. Deve-se admitir que por causa da "aprendizagem", a probabilidade de obter um resultado favorável cresça com o número de tentativas realizadas. Espe