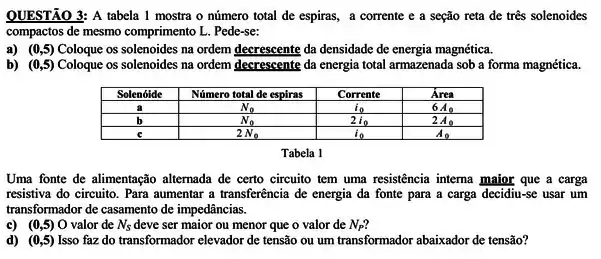
Passo 1
Letra (a). Parte 1. Antes de querer colocar em ordem vamos nos lembrar o que é densidade de energia magnética. Ela é calculada na seguinte forma:
Então, ordenar os solenoides em ordem decrescente de densidade de energia magnética é equivalente a ordenar os solenoides em ordem decrescente de campo magnético gerado.
Passo 2
Letra (a). Parte 2. Então, agora é a gente se lembrar quem é o campo magnético gerado por um solenóide. A ideia é a seguinte:
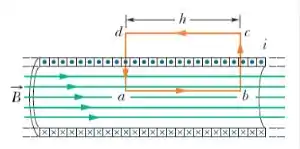
A gente pode aplicar a lei de Faraday em um solenoide genérico que nem esse da figura. A corrente interna vai valer:
O campo magnético da integral de linha ao longo da amperiana vale:
Onde é o comprimento do solenoide. Por essa razão:
Comparando os valores de “” temos que:
Assim:
Passo 3
Letra (c). Quando falamos de energia total, temos que pegar a densidade de energia e multiplicar pelo volume dos solenoides. Dessa forma:
Temos então que comparar os valores de:
Que é o que muda para cada solenoide. Fazendo isso, encontramos:
Passo 4
Queremos maior que m então e temos um abaixador de tensão. Letra (c) e (d).
Resposta
Ei, a resposta está no passo a passo :)