UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 3a
Considere o mesmo cabo coaxial da questão anterior.
Utilizando o campo calculado na questão anterior, determine a densidade de energia na região entre o cilindro e a casca.
Passo 1
Oiie tudo bem?
O sistema que a questão anterior trazia descreve um sistema que pode ser visto da seguinte forma
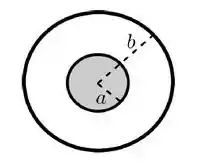
imagine que o círculo de raio é o corte transversal da casca cilíndrica e tem uma corrente que aponta para dentro da tela, e que o disco no interior é o corte transversal do cilindro maciço em seu interior com uma corrente que sai da tela! A intensidade desta corrente é tanto na superfície cilíndrica quanto no cilindro maciço, e temos a informação adicional que a corrente é uniformemente distribuída transversalmente pelo cilindro, ou seja
em que é a densidade de corrente e é uma área transversal! Esta alternativa nos pede
Utilizando o campo calculado na questão anterior, determine a densidade de energia na região entre o cilindro e a casca.
O campo que calculamos na questão anterior foi o seguinte
em que é uma coordenada radial que obedece
nós queremos obter a densidade de energia entre a casca cilíndrica e o cilindro maciço! Mas como calculamos a densidade de energia? Temos uma formulinha conhecida para isso! Saca só!
Passo 2
A densidade de energia é definida como
ou seja, só precisamos saber o formato do campo magnético! Que já obtemos na questão anterior, portanto, temos que
Essa alternativa foi isso! Vamos para a próxima agora!