UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 3c
Considere o mesmo cabo coaxial da questão anterior.
A partir do resultado acima, obtenha a auto-indutância por unidade de comprimento deste cabo. Compare com o resultado obtido na questão anterior.
Passo 1
Oiie tudo bem?
O sistema que a questão anterior trazia descreve um sistema que pode ser visto da seguinte forma
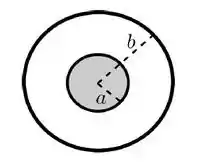
imagine que o círculo de raio é o corte transversal da casca cilíndrica e tem uma corrente que aponta para dentro da tela, e que o disco no interior é o corte transversal do cilindro maciço em seu interior com uma corrente que sai da tela! A intensidade desta corrente é tanto na superfície cilíndrica quanto no cilindro maciço, e temos a informação adicional que a corrente é uniformemente distribuída transversalmente pelo cilindro, ou seja
em que é a densidade de corrente e é uma área transversal! Esta alternativa nos pede
A partir do resultado acima, obtenha a auto-indutância por unidade de comprimento deste cabo. Compare com o resultado obtido na questão anterior.
Na alternativa anterior obtivemos que a energia total armazenada é dada por
Mas como obtemos a auto-indutância através disso? É uma questão de comparação, existe uma relação direta entre ambas as grandezas, você consegue se lembrar? Vem comigo!
Passo 2
A energia total armazenada em um indutor é dada por
ou seja, se pegarmos o resultado da alternativa anterior, obtemos que
de forma que a auto-indutância é dada por
que é exatamente o mesmo resultado obtido na questão anterior mas através de outra abordagem! A questão foi isso! Te vejo na próxima! Tchau Tchau!