A figura abaixo ilustra duas cascas cilíndricas coaxiais e muito longas (podem ser consideradas infinitas), uma de raio e outra de raio .
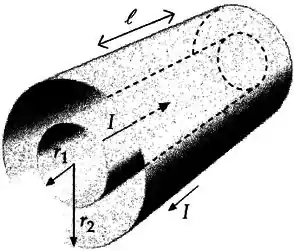
A corrente elétrica que passa em ambas as cascas cilíndricas tem intensidade , mas flui em sentidos opostos, como indicado na figura.
Para tal situação, calcule:
O módulo do campo magnético para , usando lei de Ampère.
A energia magnética armazenada num volume de comprimento na região entre as cascas.
A indutância por unidade de comprimento do sistema.
Passo 1
O módulo do campo magnético para , usando lei de Ampère.
A Lei de Ampère é dada por:
Na região , a nossa amperiana envolve apenas a corrente que passa pela casca cilíndrica de raio , logo:
Passo 2
A energia magnética armazenada num volume de comprimento na região entre as cascas.
A energia magnética é dada por:
Onde é a densidade de energia magnética:
Aplicando a expressão para o campo magnético encontrada no Passo 1, temos:
E como estamos trabalhando com geometria cilíndrica, temos que:
Portanto:
Passo 3
A indutância por unidade de comprimento do sistema.
A indutância está associada à energia magnética por:
Igualando à expressão que encontramos no Passo 2, temos:
Resposta