Um solenóide toroidal cheio de ar, com campo magnético uniforme ao longo de toda a seção reta de seu núcleo, possui espiras e um raio médio de , com seção reta de área igual a . Supondo que a corrente que passa em suas espiras seja igual a , calcule:
- O campo magnético do toróide;
- A auto-indutância do toróide;
- A energia armazenada no campo magnético;
- A densidade de energia armazenada no campo magnético.
Passo 1
Vamos tentar entender a situação do problema dando uma olhada para a figura abaixo. Se você pegar a ideia dessa questão, você mata qualquer outro problema parecido que aparecer no seu caminho...vai por mim... :-) Fica firme!!
Aqui representei para você, para ficar mais fácil de a gente ver a situação, apenas uma seção transversal de um toróide, neste caso apenas metade do toróide e apenas algumas poucas das espiras quadradas (poderiam ser circulares também, ok? Não vai importar para o que a gente vai ver neste exercício!!!).
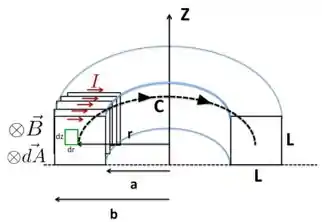
Cada uma das espiras transporta uma corrente e as colocamos no sentido horário indicado na figura. Além disso, imagina que essas espiras estão todas muuuiiitoo próximas umas das outras, o que geralmente aparece nos textos como “espiras muito compactas”.
Pela regra da mão direita, a gente sabe que o campo magnético que essas correntes geram está entrando no plano da página e esse campo fica todo dentro da região de raio . Para facilitar nossa discussão, colocamos também a área sempre paralela ao campo magnético e entrando no plano da página, como ilustrado na figura.
Passo 2
a) Lá na nossa discussão da teoria, você viu que o módulo para o campo magnético dentro do toróide tem a seguinte expressão
Fica claro dessa equação, que o campo magnético depende da distância do centro do toróide, ou seja, posições diferentes dentro das espiras tem valores diferentes para o campo magnético, blz?
Agora, existe uma situação particular, que vou te mostrar agora. Quando a gente tem , ou seja, a seção reta tem dimensões muito pequenas comparadas com a distância , a gente tem um campo uniforme dentro do toróide e podemos substituir a distância por um raio médio fixo. Isto é, na expressão do campo, podemos fazer o seguinte
que tem um valor constante e igual a em todos os pontos dentro do toróide. Fechou?? Se você substitui os valores dados no enunciado, obtém que o campo tem o valor de
Tudo que a gente vai fazer nos próximos itens vai usar esse campo constante com aí de cima. Fica ligado nisso, tá ok?
Passo 3
b) Bom, agora que já visualizamos a questão através da figura (tomara que ela tenha mesmo te ajudado com isso...rsrs), vamos entender o que precisamos calcular neste caso.
Primeiro, para obter a autoindutância do toróide, vamos começar nossa solução pela expressão do fluxo magnético e sua relação com a autoindutância dada por
sendo que é corrente que percorre cada uma das espiras do solenóide toroidal.
O caminho que a gente vai seguir abaixo é o seguinte: calculamos o fluxo total do toróide e o igualamos a para tirar a expressão para . Sacô a ideia? Segue firme...
Tendo o valor do campo gerado pela corrente que passa nas espiras, podemos encontrar o fluxo magnético. Como o vetor área é sempre paralelo a , temos que
Agora, lembra lá do enunciado que o campo é uniforme dentro do toróide? Por essa razão, a gente pode tirar o campo magnético dessa integral e já substituir o valor que temos para ele do Passo 2. Isso dá o seguinte
que nos permite encontrar a expressão para a autoindutância do toróide como
Fica ligado, porque essa expressão vale apenas para o caso em que o campo magnético dentro do toróide é uniforme, tranquilo? Guarda isso no coração...Quando não for uniforme, daí a gente vai ter que trabalhar um pouco mais, mas a gente vai te ajudar nesse caso mais geral também, já que pode cair também na sua prova...
Finalizando o item, colocamos os valores do enunciado nessa expressão e tacando na calculadora, você vai ter que
Passo 4
c) Como a energia magnética acumulada no campo magnético é dada por
temos, utilizando o valor da indutância encontrada no passo anterior, que
Passo 5
e) A energia que encontramos no passo anterior fica armazenada em um volume igual ao produto da área da seção reta do toróide vezes o comprimento do toróide que igual a , ou seja, .
Portanto, a densidade de energia, ou seja, a energia por unidade de volume, tem o seguinte valor
Esse valor diz para a gente que cada do interior do toróide tem uma energia de .