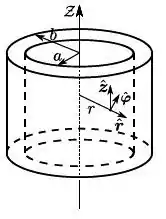
Considere um campo magnético estacionário não uniforme dado por onde é a distância do ponto de aplicação do campo magnético até um determinado eixo, é o vetor unitário circular em torno de tal eixo, e . Qual opção indica a energia por unidade de comprimento ao longo do eixo, entre duas superfícies cilíndricas coaxiais com eixo supracitado, de raios e , com ?
Passo 1
Aplicando a fórmula da densidade de energia do campo magnético:
Conseguimos a energia por comprimento se integramos na área da coroa circular:
Passo 2
Como já temos o campo, aplicando coordenadas polares (usando o macete de uma integral só):
Substituindo:
Resposta
Letra b
Exercícios de Livros Relacionados
29.75 Uma espira condutora quadrada, de lado igual a 20,0c m , é colocada no mesmo campo magnético descrito no E x e r c í c i o 29.30 í . (Veja a F i g u r a29.55 ; o centro da espira quadrada está n
56. Um capacitor de 5,0μ F possui carga inicial com potencial igual a 16,0V . A seguir, ele é conectado em séria a um indutor de 3,75m H . ( a ) Qual é a energia total armazenada nesse circuito? Qual
Um fio de cobre conduz uma corrente de 10A uniformemente distribuída em sua seção reta. Calcule a densidade de energia (a) do campo magnético e (b) do campo elétrico na superfície do fio. O diâmetro d
23- Mostre que L // R possui unidades de tempo.
27- Torne como referência o Exercício 30.19 . ( a ) Qual é a potência fornecida pela bateria para o indutor em função do tempo quando o circuito fica fechado no instante t = 0 ? ( b ) Qual é a taxa de