UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 3b
Considere o mesmo cabo coaxial da questão anterior.
Obtenha a energia total armazenada pelo campo magnético em uma porção de comprimento desta região. Sugestão: utilize como elemento de volume para integração uma casca cilíndrica de raio e espessura infinitesimal ds.
Passo 1
Oiie tudo bem?
O sistema que a questão anterior trazia descreve um sistema que pode ser visto da seguinte forma
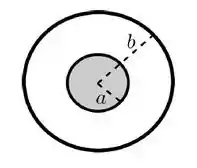
imagine que o círculo de raio é o corte transversal da casca cilíndrica e tem uma corrente que aponta para dentro da tela, e que o disco no interior é o corte transversal do cilindro maciço em seu interior com uma corrente que sai da tela! A intensidade desta corrente é tanto na superfície cilíndrica quanto no cilindro maciço, e temos a informação adicional que a corrente é uniformemente distribuída transversalmente pelo cilindro, ou seja
em que é a densidade de corrente e é uma área transversal! Esta alternativa nos pede
Obtenha a energia total armazenada pelo campo magnético em uma porção de comprimento desta região. Sugestão: utilize como elemento de volume para integração uma casca cilíndrica de raio e espessura infinitesimal ds.
lembremos que na alternativa anterior calculamos a seguinte densidade de energia
como encontramos então a energia total? Precisamos integrar ao longo de todo o cabo! Para isso faremos o que a sugestão indica, e usar um elemento superficial em coordenadas cilíndricas! E resolver a seguinte integração
Vamos escrever o nosso elemento de volume!!
Passo 2
Usando coordenadas cilíndricas, temos que o elemento de volume é da forma
e como a região é um cilindro com raio dado por
e comprimento , a nossa integral se torna
Vamos resolver as integrações!
Passo 3
A integral em resulta em
a integral em analogamente nos dá
e, por último, a integral radial se torna
De forma que a energia total armazenada é dada por
Ou seja, temos a nossa energia total! Essa alternativa foi isso! Vamos para a última!