Uma distribuição de corrente é dada pelo vetor densidade de corrente, em coordenadas cilíndricas, definido por:
para
, para ,
Onde é uma distância, e é uma constante positiva.
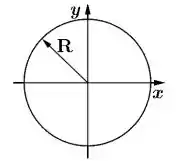
- Tomando como referência a figura ao lado, o campo magnético gerado pela densidade de corrente tem sentido horário ou anti-horário?
b) Encontre o módulo do campo magnético gerado pela densidade de corrente nas regiões e .
Passo 1
Eaee!!! Belezinha? Bom... a questão nos dá um vetor densidade de corrente (dado em coordenadas cilíndricas) junto com uma figurinha para podermos entender melhor.
Aí, ela pede para a gente dizer se o campo magnético gerado pela densidade de corrente tem sentido horário ou anti-horário.
Também, pede para encontrarmos o módulo do campo magnético gerado pela corrente nas regiões dadas.
Uma ideia é aplicarmos a regra da mão direita e também utilizarmos nossos conhecimentos sobre a Lei de Ampère, a qual diz o seguinte:
Onde é a densidade de campo magnético, é o diferencial de comprimento da amperiana, é a permeabilidade magnética e é a corrente envolvida pela amperiana.
E aí? Bora responder?
Passo 2
Bom... na figura, sabendo que o eixo está saindo do papel. Assim, podemos aplicar a regra da mão direita!
Apontando o polegar no sentido da distribuição de correntes, ou seja, saindo do papel, percebe-se que o campo magnético apresenta sentido anti-horário!!
Assim, já resolvemos a letra a)!!
Passo 3
Já na letra b), na região (região 1), podemos imaginar uma amperiana nessa região e no sentido anti-horário.
Assim, pela Lei de Ampère, temos:
Como temos a densidade de corrente em função de , vemos que a corrente envolvida pela amperiada é dada por:
Assim, substituindo na Lei de Ampère, temos:
Passo 4
Agora, para a região (região 2):
Temos que essa região corresponde a região externa do fio, portanto, a corrente envolvida pela amperiana é a corrente total do fio.
Sendo assim, temos:
Entendeu direitinho? Responde aee ;)

Resposta
- Sentido anti-horário
- Região 1:
Região 2: