Uma partícula de massa m está confinada em um poço de potencial infinito (“caixa unidimensional”), ou seja,
a) Resolva a equação de Schrödinger para encontrar os valores quantizados de energia (autovalores de energia) e as respectivas funções de onda associadas (autofunções).
b) Normalize a autofunção para o n-ésimo estado de energia. Mostre assim que, independente do nível, a constante de normalização vale .
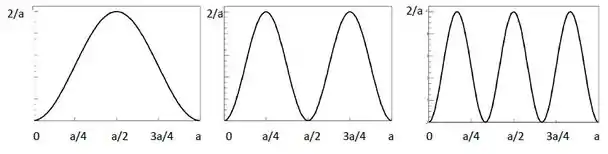
c) Faça um esboço da densidade de probabilidade para as autofunções associadas aos três primeiros níveis de energia.
d) Estando a partícula no nível, qual é a probabilidade de que seja encontrada em alguma posição entre e ?
Passo 1
a) Dentro do poço, o potencial é nulo e a equação de Schrödinger é simplesmente
Esta é uma equação diferencial cujas soluções gerais são e (ou exponenciais complexas). Escrevamos a solução geral do tipo:
Ao substituir na Eq. de Schrödinger, encontramos:
Que vemos que, de fato, é solução para . Entretanto essa ainda é uma solução genérica. Considerando que, para ou o potencial é infinito, devemos impor . Para que devemos ter (somente a componente seno obedece essa condição). Para que tem-se:
Com inteiro
Portanto, as soluções da Equação de Schrödinger são:
Estas soluções estão associadas a níveis quantizados de energia:
Passo 2
b) Normalizando a função de onda:
Substituimos e os limites de integração passam a ser e . Para fazer a integral, usamos a identidade trigonométrico . Portanto,
E vemos que este resultado independe de .
Passo 3
c) As três primeiras autofunções são ; ; . As densidades de probabilidade estão dadas por , portanto serão todas funções seno quadrado
Passo 4
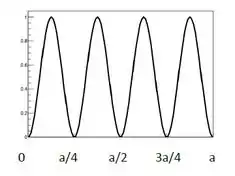
d) Essa probabilidade pode ser obtida por integração direta (como feito no item (b) para obter . Mas isto também pode ser inferido pela forma da distribuição de probabilidade (como feito na letra (c)): vê-se claramente que a probabilidade entre e é da probabilidade total:
Resposta
Letra (d):