A figura mostra, num diagrama , transformações de de gás nitrogênio () em um reservatório selado. A temperatura do gás no estado é , ou . A constante de gás ideal é , e o peso atômico do nitrogênio é igual a.
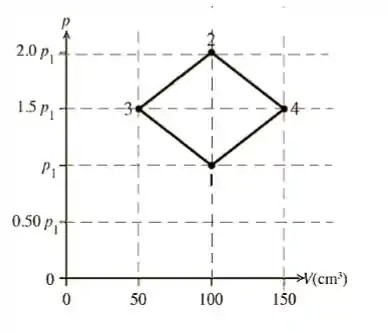
Quais são, respectivamente, a pressão do gás no estado , em unidades de , e a temperatura no estado , em °?
Uma ordenação correta das temperaturas corresponde a:
Passo 1
No estado temos a temperatura dada no enunciado , o volume que conseguimos encontrar pelo gráfico , ainda temos a massa de gás nitrogênio e sua massa atômica e som esses dois conseguimos encontrar o número de mols.
Tendo tudo isso, conseguimos descobrir a pressão no estado , utilizando a equação geral dos gases:
Passo 2
Já encontramos a , agora só falta encontrarmos a temperatura . Para isso vamos usar a equação geral dos gases novamente, porém precisamos descobrir a pressão no estado . E faremos isso pelo gráfico. Como e
Agora que descobrimos a pressão no estado , conseguimos achar a temperatura nesse estado.
Como queremos em , vamos transformar a temperatura de elvim para graus Celsius.
Assim, chegamos na alternativa
Passo 3
Já vimos que . Agora vamos analisar os estados e e para isso precisamos saber a pressão nesses estados.
Agora usando “PiViTi-PoVoTo”
Vamos relacionar as temperaturas:
Agora vamos descobrir o valor de
Assim, chegamos na seguinte relação entre as temperaturas:
O que corresponde a alternativa