Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Gases Ideais

Ver Teoria
Exercício 412356789101112131415161718192021222324252627282930313233343536373839

Enunciado

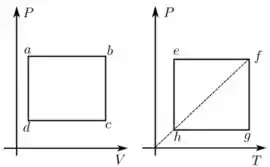
Em relação aos gráficos a seguir, que ilustram processos D I F E R E N T E S sofridos por um gás ideal, marque a alternativa correta:

a   T d < T a < T b , e V e < V f < V g .

b   T a < T b < T d , e V f < V g < V h .

c   T d < T b < T a , e V f = V h < V g .

d   T b < T d < T a , e V h < V f = V g

e   T d < T a < < T b , e V e = V f < V g .

Passo 1

Vamos analisar primeiro o ciclo da figura da esquerda. Em toda essa questão, a gente vai usar aquela relação de sempre:

P 1 V 1 T 1 = P 2 V 2 T 2

Show?

Beleza, então vamos lá:

Vamos comparar primeiro a temperatura de a com a de b . Então:

P a V a T a = P b V b T b → T b = T a . P b V b P a V a

Mas pelo gráfico, P b = P a e V b > V a , então:

T b = T a . V b V a   → T b > T a

Passo 2

Agora vamos comparar T a com T d . Assim:

P a V a T a = P d V d T d → T d = T a . P d V d P a V a

Como V a = V d e P a > P d :

T d = T a . P d V d P a V a = T a . P d P a   → T d < T a

Então, como:

T b > T a

T d < T a

Logo:

T d < T a < T b

Passo 3

Agora analisando o ciclo 2 da mesma forma:

Usando a mesma relação de novo: P 1 V 1 T 1 = P 2 V 2 T 2

Vamos resolver a parada da mesma forma. Só que agora é só a gente perceber quem são os eixos.

Comparando o volume de e com f :

P e V e T e = P f V f T f   → V f = V e P e T e . T f P f

Como P e = P f e T f > T e :

V f = V e . T f T e → V f > V e

Passo 4

Comparando V f com V g :

Usando o Piviti-Povoto de novo:

V g = V f P f T f . T g P g

Como T f = T g e P g < P f :

V g = V f . P f P g   → V g > V f

Então:

V e < V f < V g

Assim, podemos afirmar que

T d < T a < T b , e V e < V f < V g .

Resposta

a   T d < T a < T b , e V e < V f < V g .

Exercícios de Livros Relacionados

60. Um frasco com volume de 1,50L , equipado com uma válvula, contém o gás etano ( C 2 H 6 ) a 300K e à pressão atmosférica ( 1,03 ⋅ 10 5P a ) . A massa molar do etanol é 30,1g / m o l . O sistema é a
Determine a massa em quilogramas de 7,50.10 24 átomos de arsênio, que tem uma massa molar de 74,9g / m o l .
Um pneu de automóvel tem um volume de 1,64.10 - 2m 3 e contém ar à pressão manométrica (pressão acima da pressão atmosférica) de 165k P a quando a temperatura é 0,00° C . Qual é a pressão manométrica
Uma amostra de oxigênio com um volume de 1000c m 3 a 40,0° C e 1,01.10 5P a se expande até um volume de 1500c m 3 a uma pressão de 1,06.10 5P a . Determine (a) o número de mols de oxigênio presentes n
Você copia o seguinte parágrafo de um livro de física marciano: "1 snorf de um gás ideal ocupa um volume de 1,35 Zaks. A uma temperatura de 22 glips, o gás tem uma pressão de 12,5 klads. A uma tempera